1. Introduction
The value definition field of each CSS property can contain keywords, data types (which appear between < and >), and information on how they can be combined. Generic data types (<length> being the most widely used) that can be used by many properties are described in this specification, while more specific data types (e.g., <spacing-limit>) are described in the corresponding modules.
1.1. Module Interactions
This module replaces and extends the data type definitions in [CSS2] sections 1.4.2.1, 4.3, and A.2.
2. Value Definition Syntax
The value definition syntax described here is used to define the set of valid values for CSS properties (and the valid syntax of many other parts of CSS). A value so described can have one or more components.
2.1. Component Value Types
Component value types are designated in several ways:
-
Keyword values (such as auto, disc, etc.), which appear literally, without quotes (e.g.
auto). -
Basic data types, which appear between < and > (e.g., <length>, <percentage>, etc.). For numeric data types, this type notation can annotate any range restrictions using the bracketed range notation described below.
-
Property value ranges, which represent the same pattern of values as a property bearing the same name. These are written as the property name, surrounded by single quotes, between < and >, e.g., <'border-width'>, <'background-attachment'>, etc.
These types do not include CSS-wide keywords such as inherit. Additionally, if the property’s value grammar is a comma-separated repetition, the corresponding type does not include the top-level comma-separated list multiplier. (E.g. if a property named pairing is defined as [ <custom-ident> <integer>? ]#, then <'pairing'> is equivalent to [ <custom-ident> <integer>? ], not [ <custom-ident> <integer>? ]#.)\
Why remove the multiplier?
The top-level multiplier is ripped out of these value types because top-level comma-separated repetitions are mostly used for coordinating list properties, and when a shorthand combines several such properties, it needs the unmultiplied grammar so it can construct its own comma-separated repetition.
Without this special treatment, every such longhand would have to be defined with an ad-hoc production just for the inner value, which makes the grammars harder to understand overall.
-
Functional notations and their arguments. These are written as the function’s name, followed by an empty parentheses pair, between < and >, e.g. <calc()>, and references the correspondingly-named functional notation.
-
Other non-terminals. These are written as the name of the non-terminal between < and >, as in <spacing-limit>. Notice the distinction between <border-width> and <'border-width'>: the latter represents the grammar of the border-width property, the former requires an explicit expansion elsewhere. The definition of a non-terminal is typically located near its first appearance in the specification.
Some property value definitions also include the slash (/), the comma (,), and/or parentheses as literals. These represent their corresponding tokens. Other non-keyword literal characters that may appear in a component value, such as “+”, must be written enclosed in single quotes.
Commas specified in the grammar are implicitly omissible in some circumstances, when used to separate optional terms in the grammar. Within a top-level list in a property or other CSS value, or a function’s argument list, a comma specified in the grammar must be omitted if:
- all items preceding the comma have been omitted
- all items following the comma have been omitted
- multiple commas would be adjacent (ignoring white space/comments), due to the items between the commas being omitted.
example ( first?, second?, third?)
Given this grammar, writing example(first, second, third) is valid, as is example(first, second) or example(first, third) or example(second). However, example(first, , third) is invalid, as one of those commas are no longer separating two options; similarly, example(,second) and example(first,) are invalid. example(first second) is also invalid, as commas are still required to actually separate the options.
If commas were not implicitly omittable, the grammar would have to be much more complicated to properly express the ways that the arguments can be omitted, greatly obscuring the simplicity of the feature.
All CSS properties also accept the CSS-wide keyword values as the sole component of their property value.
For readability these are not listed explicitly in the property value syntax definitions.
For example, the full value definition of border-color under CSS Cascading and Inheritance Level 3 is <color> (even though it is listed as <color>).
Note: This implies that, in general, combining these keywords with other component values in the same declaration results in an invalid declaration. For example, background: url(corner.png) no-repeat, inherit; is invalid.
2.2. Component Value Combinators
Component values can be arranged into property values as follows:
- Juxtaposing components means that all of them must occur, in the given order.
- A double ampersand (&&) separates two or more components, all of which must occur, in any order.
- A double bar (||) separates two or more options: one or more of them must occur, in any order.
- A bar (|) separates two or more alternatives: exactly one of them must occur.
- Brackets ([ ]) are for grouping.
Juxtaposition is stronger than the double ampersand, the double ampersand is stronger than the double bar, and the double bar is stronger than the bar. Thus, the following lines are equivalent:
a b | c || d && e f[ a b] |[ c ||[ d &&[ e f]]]
For reorderable combinators (||, &&), ordering of the grammar does not matter: components in the same grouping may be interleaved in any order. Thus, the following lines are equivalent:
a || b || c b || a || c
Note: Combinators are not associative, so grouping is significant. For example, a || b || c and a || [ b || c ] are distinct grammars: the first allows a value like b a c, but the second does not.
2.3. Component Value Multipliers
Every type, keyword, or bracketed group may be followed by one of the following modifiers:
- An asterisk (*) indicates that the preceding type, word, or group occurs zero or more times.
- A plus (+) indicates that the preceding type, word, or group occurs one or more times.
- A question mark (?) indicates that the preceding type, word, or group is optional (occurs zero or one times).
- A single number in curly braces ({A}) indicates that the preceding type, word, or group occurs A times.
- A comma-separated pair of numbers in curly braces ({A,B}) indicates that the preceding type, word, or group occurs at least A and at most B times. The B may be omitted ({A,}) to indicate that there must be at least A repetitions, with no upper bound on the number of repetitions.
- A hash mark (#) indicates that the preceding type, word, or group occurs one or more times, separated by comma tokens (which may optionally be surrounded by white space and/or comments). It may optionally be followed by the curly brace forms, above, to indicate precisely how many times the repetition occurs, like <length>#{1,4}.
- An exclamation point (!) after a group indicates that the group is required and must produce at least one value; even if the grammar of the items within the group would otherwise allow the entire contents to be omitted, at least one component value must not be omitted.
The + and # multipliers may be stacked as +#; similarly, the # and ? multipliers may be stacked as #?. These stacks each represent the later multiplier applied to the result of the earlier multiplier. (These same stacks can be represented using grouping, but in complex grammars this can push the number of brackets beyond readability.)
For repeated component values (indicated by *, +, or #), UAs must support at least 20 repetitions of the component. If a property value contains more than the supported number of repetitions, the declaration must be ignored as if it were invalid.
2.4. Combinator and Multiplier Patterns
There are a small set of common ways to combine multiple independent component values in particular numbers and orders. In particular, it’s common to want to express that, from a set of component value, the author must select zero or more, one or more, or all of them, and in either the order specified in the grammar or in any order.
All of these can be easily expressed using simple patterns of combinators and multipliers:
| in order | any order | |
|---|---|---|
| zero or more | A? B? C?
| A? || B? || C?
|
| one or more | | A || B || C
|
| all | A B C
| A && B && C
|
Note that all of the "any order" possibilities are expressed using combinators, while the "in order" possibilities are all variants on juxtaposition.
2.5. Component Values and White Space
Unless otherwise specified, white space and/or comments may appear before, after, and/or between components combined using the above combinators and multipliers.
Note: In many cases, spaces will in fact be required between components in order to distinguish them from each other. For example, the value 1em2em would be parsed as a single <dimension-token> with the number 1 and the identifier em2em, which is an invalid unit. In this case, a space would be required before the 2 to get this parsed as the two lengths 1em and 2em.
2.6. Functional Notation Definitions
The syntax of a functional notation is defined as a sequence of:
-
The function’s name written as an identifier followed by an open parenthesis (such as example(), or the <function-token> production to indicate a function with an arbitrary name.
-
The function’s arguments, if any, expressed using the value definition syntax.
-
A literal closing parenthesis.
The function’s arguments are considered implicitly grouped, as if surrounded by brackets ([ ... ]).
example ( <length>, <length>)
will match a function whose name is "example" and whose arguments match "<length> , <length>".
<pseudo-class-selector> =':' <ident-token> |':' <function-token> <any-value>')'
This represents any function name, with <any-value> as the function arguments.
2.7. Property Value Examples
Below are some examples of properties with their corresponding value definition fields
| Property | Value definition field | Example value |
|---|---|---|
| orphans | <integer> | 3 |
| text-align | left | right | center | justify | center |
| padding-top | <length> | <percentage> | 5% |
| outline-color | <color> | invert | #fefefe |
| text-decoration | none | underline || overline || line-through || blink | overline underline |
| font-family | [ <family-name> | <generic-family> ]# | "Gill Sans", Futura, sans-serif |
| border-width | [ <length> | thick | medium | thin ]{1,4} | 2px medium 4px |
| box-shadow | [ inset? && <length>{2,4} && <color>? ]# | none | 3px 3px rgba(50%, 50%, 50%, 50%), lemonchiffon 0 0 4px inset |
2.8. Non-Terminal Definitions and Grammar Production Blocks
The precise grammar of non-terminals, like <position> or <calc()>, is often specified in a CSS grammar production block. These are conventionally represented in a preformatted block of definitions like this:
<foo> = keyword | <bar> | some-really-long-pattern-of-stuff <bar> = <length>
Each definition starts on its own line,
and consists of the non-terminal to be defined,
followed by an =,
followed by the fragment of value definition syntax to which it expands.
A definition can stretch across multiple lines,
and terminates before the next line that starts a new grammar production
or at the end of the grammar production block
(whichever comes first).
= is never valid in value definition syntax,
so it’s unambiguous when a new line starts a fresh definition.) 3. Combining Values: Interpolation, Addition, and Accumulation
Some procedures, for example transitions and animations, combine two CSS property values. The following combining operations—on the two computed values VA and VB yielding the computed value Vresult—are defined. For operations that are not commutative (for example, matrix multiplication, or accumulation of mismatched transform lists) VA represents the first term of the operation and VB represents the second.
- interpolation
-
Given two property values VA and VB,
produces an intermediate value Vresult at a distance of p along the interval between VA and VB such that p = 0 produces VA and p = 1 produces VB.
The range of p is (−∞, ∞) due to the effect of timing functions. As a result, this procedure must also define extrapolation behavior for p outside [0, 1].
- addition
-
Given two property values VA and VB,
returns the sum of the two properties, Vresult.
Note: While addition can often be expressed in terms of the same weighted sum function used to define interpolation, this is not always the case. For example, interpolation of transform matrices involves decomposing and interpolating the matrix components whilst addition relies on matrix multiplication.
If a value type does not define a specific procedure for addition or is defined as not additive, its addition operation is simply Vresult = VB.
- accumulation
-
Given two property values VA and VB,
returns the result, Vresult,
of combining the two operands
such that VB is treated as a delta from VA.
Note: For many types of animation such as numbers or lengths, accumulation is defined to be identical to addition.
A common case where the definitions differ is for list-based types where addition may be defined as appending to a list whilst accumulation may be defined as component-based addition. For example, the filter list values blur(2) and blur(3), when added together would produce blur(2) blur(3), but when accumulated would produce blur(5).
If a value type does not define a specific procedure for accumulation, its accumulation operation is identical to addition.
These operations are only defined on computed values. (As a result, it is not necessary to define, for example, how to add a <length> value of 15pt with 5em since such values will be resolved to their canonical unit before being passed to any of the above procedures.)
3.1. Range Checking
Interpolation can result in a value outside the valid range for a property, even if all of the inputs to interpolation are valid; this especially happens when p is outside the [0, 1] range, but some easing functions can cause this to occur even within that range. If the final result after interpolation, addition, and accumulation is out-of-range for the target context the value is being used in, it does not cause the declaration to be invalid. Instead, the value must be clamped to the range allowed in the target context, exactly the same as math functions (see § 10.12 Range Checking).
Note: Even if interpolation results in an out-of-range value, addition/accumulation might "correct" the result and bring it back into range. Thus, clamping is only applied to the final result of applying all interpolation-related operations.
4. Textual Data Types
The textual data types include various keywords and identifiers as well as strings (<string>) and URLs (<url>). Aside from the casing of pre-defined keywords or as explicitly defined for a given property, no normalization is performed, not even Unicode normalization: the specified and computed value of a property are exactly the provided Unicode values after parsing (which includes character set conversion and escaping). [UNICODE] [CSS-SYNTAX-3]
CSS identifiers, generically denoted by <ident>, consist of a sequence of characters conforming to the <ident-token> grammar. [CSS-SYNTAX-3] Identifiers cannot be quoted; otherwise they would be interpreted as strings. CSS properties accept two classes of identifiers: pre-defined keywords and author-defined identifiers.
Note: The <ident> production is not meant for property value definitions—<custom-ident> should be used instead. It is provided as a convenience for defining other syntactic constructs.
All textual data types interpolate as discrete and are not additive.
4.1. Pre-defined Keywords
In the value definition fields, keywords with a pre-defined meaning appear literally. Keywords are identifiers and are interpreted ASCII case-insensitively (i.e., [a-z] and [A-Z] are equivalent).
Value : collapse | separate
And here is an example of its use:
table{ border-collapse : separate}
4.1.1. CSS-wide keywords: initial, inherit and unset
As defined above, all properties accept the CSS-wide keywords, which represent value computations common to all CSS properties. These keywords are normatively defined in the CSS Cascading and Inheritance Module.
Tests
Other CSS specifications can define additional CSS-wide keywords.
4.2. Unprefixed Author-defined Identifiers: the <custom-ident> type
Some properties accept arbitrary author-defined identifiers as a component value. This generic data type is denoted by <custom-ident>, and represents any valid CSS identifier that would not be misinterpreted as a pre-defined keyword in that property’s value definition. Such identifiers are fully case-sensitive (meaning they’re compared using the "identical to" operation), even in the ASCII range (e.g. example and EXAMPLE are two different, unrelated user-defined identifiers).
The CSS-wide keywords are not valid <custom-ident>s. The default keyword is reserved and is also not a valid <custom-ident>. Specifications using <custom-ident> must specify clearly what other keywords are excluded from <custom-ident>, if any—for example by saying that any pre-defined keywords in that property’s value definition are excluded. Excluded keywords are excluded in all ASCII case permutations.
When parsing positionally-ambiguous keywords in a property value, a <custom-ident> production can only claim the keyword if no other unfulfilled production can claim it.
Note: When designing grammars with <custom-ident>, the <custom-ident> should always be “positionally unambiguous”, so that it’s impossible to conflict with any keyword values in the property. Such conflicts can alternatively be avoided by using <dashed-ident>.
4.3. Prefixed Author-defined Identifiers: the <dashed-ident> type
Some contexts accept both author-defined identifiers and CSS-defined identifiers. If not handled carefully, this can result in difficulties adding new CSS-defined values; UAs have to study existing usage and gamble that there are sufficiently few author-defined identifiers in use matching the new CSS-defined one, so giving the new value a special CSS-defined meaning won’t break existing pages.
While there are many legacy cases in CSS that mix these two values spaces in exactly this fraught way, the <dashed-ident> type is meant to be an easy way to distinguish author-defined identifiers from CSS-defined identifiers.
The <dashed-ident> production is a <custom-ident>, with all the case-sensitivity that implies, with the additional restriction that it must start with two dashes (U+002D HYPHEN-MINUS).
<dashed-ident>s are reserved solely for use as author-defined names. CSS will never define a <dashed-ident> for its own use.
.foo{ --fg-color : blue; }
@color-profile --foo{ src : url ( https://example.com/foo.icc ); } .foo{ color : color ( --foo1 0 .5 /.2 ); }
For example, if a CSS preprocessor added a new "custom" at-rule, it shouldn’t spell it @custom, as this would clash with a future official @custom rule added by CSS. Instead, it should use @--custom, which is guaranteed to never clash with anything defined by CSS.
Even better, it should use @--library1-custom, so that if Library2 adds their own "custom" at-rule (spelled @--library2-custom), there’s no possibility of clash. Ideally this prefix should be customizable, if allowed by the tooling, so authors can manually avoid clashes on their own.
4.4. Quoted Strings: the <string> type
Strings are denoted by <string>. When written literally, they consist of a sequence of characters delimited by double quotes or single quotes, corresponding to the <string-token> production in the CSS Syntax Module [CSS-SYNTAX-3].
"\" ""\22" '\' ''\27' content : "this is a 'string'." ; content : "this is a \" string\"." ; content : 'this is a "string".' ; content : 'this is a \' string\'.'
It is possible to break strings over several lines, for aesthetic or other reasons, but in such a case the newline itself has to be escaped with a backslash (\). The newline is subsequently removed from the string. For instance, the following two selectors are exactly the same:
Since a string cannot directly represent a newline, to include a newline in a string, use the escape "\A". (Hexadecimal A is the line feed character in Unicode (U+000A), but represents the generic notion of "newline" in CSS.)
4.5. Resource Locators: the <url> type
The <url> type, written with the url() and src() functions, represents a URL, which is a pointer to a resource.
The syntax of <url> is:
<url> = <url () > | <src () > <url () > =url ( <string> <url-modifier> * ) | <url-token> <src () > =src ( <string> <url-modifier>*)
body{ background : url ( "http://www.example.com/pinkish.gif" ) }
A url() can be written without quotation marks around the URL value, in which case it is specially-parsed as a <url-token>; see CSS Syntax 3 § 4.3.6 Consume a url token. [CSS-SYNTAX-3]
Note: Because of this special parsing, url() can only express its value literally. To provide a URL by functions such as var(), use the src() notation, which does not have this special parsing rule.
background : url ( "http://www.example.com/pinkish.gif" ); background : url ( http://www.example.com/pinkish.gif );
And these have the same meaning as well:
background : src ( "http://www.example.com/pinkish.gif" ); --foo : "http://www.example.com/pinkish.gif" ; background : src ( var ( --foo));
But this does not work:
--foo : "http://www.example.com/pinkish.gif" ; background : url ( var(--foo ));
...because the unescaped "(" in the value causes a parse error, so the entire declaration is thrown out as invalid.
Note: The unquoted url() syntax cannot accept a <url-modifier> argument and has extra escaping requirements: parentheses, whitespace characters, single quotes (') and double quotes (") appearing in a URL must be escaped with a backslash, e.g. url(open\(parens), url(close\)parens). (In quoted <string> url()s, only newlines and the character used to quote the string need to be escaped.) Depending on the type of URL, it might also be possible to write these characters as URL-escapes (e.g. url(open%28parens) or url(close%29parens)) as described in [URL].
Some CSS contexts (such as @import) also allow a <url> to be represented by a bare <string>, without the function wrapper. In such cases the string behaves identically to a url() function containing that string.
@import url ( "base-theme.css" ); @import "base-theme.css" ;
4.5.1. Relative URLs
In order to create modular style sheets that are not dependent on the absolute location of a resource, authors should use relative URLs. Relative URLs (as defined in [URL]) are resolved to full URLs using a base URL. RFC 3986, section 3, defines the normative algorithm for this process. For CSS style sheets, the base URL is that of the style sheet itself, not that of the styled source document. Style sheets embedded within a document have the base URL associated with their container.
Note: For HTML documents, the base URL is mutable.
When a <url> appears in the computed value of a property, it is resolved to an absolute URL, as described in the preceding paragraph. The computed value of a URL that the UA cannot resolve to an absolute URL is the specified value.
body{ background : url ( "tile.png" ) }
is located in a style sheet designated by the URL:
http : //www.example.org/style/basic.css
The background of the source document’s <body> will be tiled with whatever image is described by the resource designated by the URL:
http : //www.example.org/style/tile.png
The same image will be used regardless of the URL of the source document containing the <body>.
4.5.1.1. Fragment URLs
To enable element ID references to work in CSS regardless of base URL changes or shadow DOM, <url>s have special behavior when they contain only a fragment.
If a <url>’s value starts with a U+0023 NUMBER SIGN (#) character,
then the URL additionally has its local url flag set,
and is a tree-scoped reference for the URL’s fragment.
When matching a <url> with the local url flag set:
-
if the URL’s fragment is an element ID reference (rather than, say, a media fragment), resolve it as a tree-scoped reference with the tree’s IDs as the associated tree-scoped names: specifically, resolve to the first element in tree order among the associated node tree's descendants with the URL’s fragment as its ID. (And, as usual for tree-scoped references, continuing up to the host’s tree if needed.)
If no such element is found, the URL fails to resolve.
-
otherwise, resolve the fragment against the current document.
Possibly reference find a potential indicated element,
but that is defined specifically for Documents,
not ShadowRoots.
Note: This means that such fragments will resolve
against the contents of the current document
(or whichever node tree the stylesheet lives in,
if shadow DOM is involved)
regardless of how such relative URLs would resolve elsewhere
(ignoring, for example, base elements
changing the base URL,
or relative URLs in linked stylesheets
resolving against the stylesheet’s URL).
#anchor will resolve against http : //example.com/#image will resolve against the elements in the HTML document itself:
<!DOCTYPE html> < base href = "http://example.com/" > ...< a href = "#anchor" style = "background-image: url(#image)" > link</ a >
When serializing a url() with the local url flag set, it must serialize as just the fragment.
4.5.2. Empty URLs
If the value of the <url> is the empty string (like url("") or url()), the url must resolve to an invalid resource (similar to what the url about:invalid does).
Its computed value is url("") or src(""), whichever was specified, and it must serialize as such.
Tests
Note: This matches the behavior of empty urls for embedded resources elsewhere in the web platform, and avoids excess traffic re-requesting the stylesheet or host document due to editing mistakes leaving the url() value empty, which are almost certain to be invalid resources for whatever the url() shows up in. Linking on the web platform does allow empty urls, so if/when CSS gains some functionality to control hyperlinks, this restriction can be relaxed in those contexts.
4.5.3. URL Modifiers
<url>s support specifying additional <url-modifier>s, which change the meaning or the interpretation of the URL somehow. A <url-modifier> is either an <ident> or a functional notation.
This specification does not define any <url-modifier>s, but other specs may do so.
Note: A <url> that is either unquoted or not wrapped in url() notation cannot accept any <url-modifier>s.
4.5.4. URL Processing Model
CSSStyleSheet sheet,
a string destination matching a RequestDestination,
a "no-cors" or "cors" corsMode,
and an algorithm processResponse accepting a response and a null, failure or byte stream:
-
Let environmentSettings be sheet’s relevant settings object.
-
Let base be sheet’s stylesheet base URL if it is not null, otherwise environmentSettings’s API base URL. [CSSOM]
-
Let parsedUrl be the result of the URL parser steps with urlValue’s url and base. If the algorithm returns an error, return.
-
Let req be a new request whose url is parsedUrl, whose destination is destination, mode is corsMode, origin is environmentSettings’s origin, credentials mode is "same-origin", use-url-credentials flag is set, client is environmentSettings, and whose referrer is environmentSettings’s API base URL.
-
Apply any URL request modifier steps that apply to this request.
Note: This specification does not define any URL request modification steps, but other specs may do so.
-
If req’s mode is "cors", set req’s referrer to sheet’s location. [CSSOM]
-
If sheet’s origin-clean flag is set, set req’s initiator type to "css". [CSSOM]
-
Fetch req, with processresponseconsumebody set to processResponse.
When interpreting URLs expressed in CSS, the URL parser’s encoding argument must be omitted (i.e. use the default, UTF-8), regardless of the stylesheet encoding.
Note: In other words, a URL written in CSS will always percent-encode non-ASCII codepoints using UTF-8 in the URL object (and thus whenever using the URL value for e.g. network requests), regardless of the stylesheet’s own encoding. Note that this occurs after decoding the stylesheet into Unicode code points.
5. Numeric Data Types
Numeric data types are used to represent quantities, indexes, positions, and other such values. Although many syntactic variations can exist in expressing the quantity (numeric aspect) in a given numeric value, the specified and computed value do not distinguish these variations: they represent the value’s abstract quantity, not its syntactic representation.
The numeric data types include <integer>, <number>, <percentage>, and various dimensions including <length>, <angle>, <time>, <frequency>, and <resolution>.
Note: While general-purpose dimensions are defined here, some other modules define additional data types (e.g. [css-grid-1] introduces fr units) whose usage is more localized.
The precision and supported range of numeric values in CSS is implementation-defined, and can vary based on the property or other context a value is used in. However, within the CSS specifications, infinite precision and range is assumed. When a value cannot be explicitly supported due to range/precision limitations, it must be converted to the closest value supported by the implementation, but how the implementation defines "closest" is implementation-defined as well.
If an <angle> must be converted due to exceeding the implementation-defined range of supported values, it must be clamped to the nearest supported multiple of 360deg.
5.1. Range Restrictions and Range Definition Notation
Properties can restrict numeric values to some range.
If the value is outside the allowed range,
then unless otherwise specified,
the declaration is invalid and must be ignored.
Range restrictions can be annotated in the numeric type notation
using CSS bracketed range notation—
Note: CSS values generally do not allow open ranges; thus only square-bracket notation is used.
CSS theoretically supports infinite precision and infinite ranges for all value types; however in reality implementations have finite capacity. UAs should support reasonably useful ranges and precisions. Range extremes that are ideally unlimited are indicated using ∞ or −∞ as appropriate. For example, <length [0,∞]> indicates a non-negative length.
If no range is indicated,
either by using the bracketed range notation or in the property description,
then
Values of −∞ or ∞ must be written without units, even if the value type uses units. Values of 0 can be written without units, even if the value type doesn’t allow “unitless zeroes” (such as <time>).
Note: At the time of writing,
the bracketed range notation is new;
thus in most CSS specifications
any range limitations are described only in prose.
(For example, “Negative values are not allowed” or
“Negative values are invalid”
indicate a
5.2. Integers: the <integer> type
Integer values are denoted by <integer>.
When written literally, an integer is one or more decimal digits 0 through 9 and corresponds to a subset of the <number-token> production in the CSS Syntax Module [CSS-SYNTAX-3]. The first digit of an integer may be immediately preceded by - or + to indicate the integer’s sign.
Tests
Unless otherwise specified, in the CSS specifications rounding to the nearest integer requires rounding in the direction of +∞ when the fractional portion is exactly 0.5. (For example, 1.5 rounds to 2, while -1.5 rounds to -1.)
5.2.1. Computation and Combination of <integer>
Unless otherwise specified, the computed value of a specified <integer> is the specified abstract integer.
Interpolation of <integer> is defined as Vresult = round((1 - p) × VA + p × VB); that is, interpolation happens in the real number space as for <number>s, and the result is converted to an <integer> by rounding to the nearest integer.
Addition of <integer> is defined as Vresult = VA + VB
5.3. Real Numbers: the <number> type
Number values are denoted by <number>, and represent real numbers, possibly with a fractional component.
Tests
- animation-iteration-count-calc.html (live test) (source)
- numbers-units-002.xht (visual test) (source)
- numbers-units-003.xht (live test) (source)
When written literally, a number is either an integer, or zero or more decimal digits followed by a dot (.) followed by one or more decimal digits; optionally, it can be concluded by the letter “e” or “E” followed by an integer indicating the base-ten exponent in scientific notation. It corresponds to the <number-token> production in the CSS Syntax Module [CSS-SYNTAX-3]. As with integers, the first character of a number may be immediately preceded by - or + to indicate the number’s sign.
The value <zero> represents a literal number with the value 0. Expressions that merely evaluate to a <number> with the value 0 (for example, calc(0)) do not match <zero>; only literal <number-token>s do.
5.3.1. Computation and Combination of <number>
Unless otherwise specified, the computed value of a specified <number> is the specified abstract number.
Interpolation of <number> is defined as Vresult = (1 - p) × VA + p × VB
Addition of <number> is defined as Vresult = VA + VB
5.4. Numbers with Units: dimension values
The general term dimension refers to a number with a unit attached to it; and is denoted by <dimension>.
When written literally, a dimension is a number immediately followed by a unit identifier, which is an identifier. It corresponds to the <dimension-token> production in the CSS Syntax Module [CSS-SYNTAX-3]. Like keywords, unit identifiers are ASCII case-insensitive.
CSS uses <dimension>s to specify distances (<length>), durations (<time>), frequencies (<frequency>), resolutions (<resolution>), and other quantities.
5.4.1. Compatible Units
When serializing computed values [CSSOM], compatible units (those related by a static multiplicative factor, like the 96:1 factor between px and in, or the computed font-size factor between em and px) are converted into a single canonical unit. Each group of compatible units defines which among them is the canonical unit that will be used for serialization.
When serializing resolved values that are used values, all value types (percentages, numbers, keywords, etc.) that represent lengths are considered compatible with lengths. Likewise any future API that returns used values must consider any values that represent distances/durations/frequencies/etc. as compatible with the relevant class of dimensions, and canonicalize accordingly.
5.4.2. Combination of Dimensions
Interpolation of compatible dimensions (for example, two <length> values) is defined as Vresult = (1 - p) × VA + p × VB
Addition of compatible dimensions is defined as Vresult = VA + VB
5.5. Percentages: the <percentage> type
Percentage values are denoted by <percentage>, and indicates a value that is some fraction of another reference value.
When written literally, a percentage consists of a number immediately followed by a percent sign %. It corresponds to the <percentage-token> production in the CSS Syntax Module [CSS-SYNTAX-3].
Percentage values are always relative to another quantity, for example a length. Each property that allows percentages also defines the quantity to which the percentage refers. This quantity can be a value of another property for the same element, the value of a property for an ancestor element, a measurement of the formatting context (e.g., the width of a containing block), or something else.
5.5.1. Computation and Combination of <percentage>
Unless otherwise specified (such as in font-size, which computes its <percentage> values to <length>), the computed value of a percentage is the specified percentage.
Interpolation of <percentage> is defined as Vresult = (1 - p) × VA + p × VB
Addition of <percentage> is defined as Vresult = VA + VB
5.6. Mixing Percentages and Dimensions
In cases where a <percentage> can represent the same quantity as a dimension in the same component value position, and can therefore be combined with them in a calc() expression, the following convenience notations may be used in the property grammar:
- <length-percentage>
-
Equivalent to
[ <length> | <percentage>] - <frequency-percentage>
-
Equivalent to
[ <frequency> | <percentage>] - <angle-percentage>
-
Equivalent to
[ <angle> | <percentage>] - <time-percentage>
-
Equivalent to
[ <time> | <percentage>]
On the other hand, the second and third arguments of the hsl() function can only be expressed as <percentage>s. Although calc() productions are allowed in their place, they can only combine percentages with themselves, as in calc(10% + 20%).
Note: Specifications should never alternate <percentage> in place of a dimension in a grammar unless they are compatible.
Note: More <type-percentage> productions can be added in the future as needed. A <number-percentage> will never be added, as <number> and <percentage> can’t be combined in calc().
5.6.1. Computation and Combination of Percentage and Dimension Mixes
The computed value of a percentage-dimension mix is defined as
-
a computed dimension if the percentage component is zero or is defined specifically to compute to a dimension value
-
a computed percentage if the dimension component is zero
-
a computed calc() expression otherwise
Interpolation of percentage-dimension value combinations (e.g. <length-percentage>, <frequency-percentage>, <angle-percentage>, <time-percentage> or equivalent notations) is defined as
- equivalent to interpolation of <length> if both VA and VB are pure <length> values
- equivalent to interpolation of <percentage> if both VA and VB are pure <percentage> values
- equivalent to converting both values into a calc() expression representing the sum of the dimension type and a percentage (each possibly zero) and interpolating each component individually (as a <length>/<frequency>/<angle>/<time> and as a <percentage>, respectively)
Addition of <percentage> is defined the same as interpolation except by adding each component rather than interpolating it.
5.7. Ratios: the <ratio> type
Ratio values are denoted by <ratio>, and represent the ratio of two numeric values. It most often represents an aspect ratio, relating a width (first) to a height (second).
When written literally, a ratio has the syntax:
<ratio> = <number[ 0 , ∞] >[ / <number[ 0 , ∞] >] ?
The second <number> is optional, defaulting to 1. However, <ratio> is always serialized with both components.
The computed value of a <ratio> is the pair of numbers provided.
If either number in the <ratio> is 0 or infinite, it represents a degenerate ratio (and, generally, won’t do anything).
If two <ratio>s need to be compared, divide the first number by the second, and compare the results. For example, 3/2 is less than 2/1, because it resolves to 1.5 while the second resolves to 2. (In other words, “tall” aspect ratios are less than “wide” aspect ratios.)
5.7.1. Combination of <ratio>
The interpolation of a <ratio> is defined by converting each <ratio> to a number by dividing the first value by the second (so a ratio of 3 / 2 would become 1.5), taking the logarithm of that result (so the 1.5 would become approximately 0.176), then interpolating those values. The result during the interpolation is converted back to a <ratio> by inverting the logarithm, then interpreting the result as a <ratio> with the result as the first value and 1 as the second value.
If either <ratio> is degenerate, the values cannot be interpolated.
start =log ( 5 ); // ≈0.69897 end =log ( 1.5 ); // ≈0.17609 interp =0.69897 *.5 +0.17609 *.5 ; // ≈0.43753 final =10 ^interp; // ≈2.73
Note: Interpolating over the logarithm of the ratio means the results are scale-independent (5 / 1 to 300 / 200 would give the same results as above), that they’re symmetrical over "wide" and "tall" variants (interpolating from 1 / 5 to 2 / 3 would give a ratio approximately equal to 1 / 2.73 at the halfway point), and that they’re symmetrical over whether the width is fixed and the height is based on the ratio or vice versa. These properties are not shared by many other possible interpolation strategies.
Note: Due to the properties of logarithms, any log can be used; the example here uses base-10 log, but if, say, the natural log and e was used, the intermediate results would be different but the final result would be the same.
Addition of <ratio>s is not possible.
6. Distance Units: the <length> type
Lengths refer to distance measurements and are denoted by <length> in the property definitions. A length is a dimension.
For zero lengths the unit identifier is optional (i.e. can be syntactically represented as the <number> 0). However, if a 0 could be parsed as either a <number> or a <length> in a property (such as line-height), it must parse as a <number>.
Properties may restrict the length value to some range. If the value is outside the allowed range, the declaration is invalid and must be ignored.
Tests
While some properties allow negative length values, this may complicate the formatting and there may be implementation-specific limits. If a negative length value is allowed but cannot be supported, it must be converted to the nearest value that can be supported.
In cases where the used length cannot be supported, user agents must approximate it in the actual value.
There are two types of length units: relative and absolute. The specified value of a length (specified length) is represented by its quantity and its unit. The computed value of a length (computed length) is the specified length resolved to an absolute length, and its unit is not distinguished: it can be represented by any absolute length unit (but will be serialized using its canonical unit, px).
Tests
- calc-unit-analysis.html (live test) (source)
- shape-outside-circle-002.html (live test) (source)
- shape-outside-circle-004.html (live test) (source)
- shape-outside-ellipse-002.html (live test) (source)
- shape-outside-ellipse-004.html (live test) (source)
- shape-outside-inset-003.html (live test) (source)
- shape-outside-polygon-004.html (live test) (source)
While the exact supported precision of numeric values, and how they are rounded to match that precision, is generally implementation-defined, <length>s in border-width and a few other properties are rounded in a specific fashion to ensure reasonable visual display. (This algorithm is called by individual properties explicitly.)
-
Assert: len is non-negative.
-
If len is an integer number of device pixels, do nothing.
-
If len is greater than zero, but less than 1 device pixel, round len up to 1 device pixel.
-
If len is greater than 1 device pixel, round it down to the nearest integer number of device pixels.
6.1. Relative Lengths
Relative length units specify a length relative to another length. Style sheets that use relative units can more easily scale from one output environment to another.
The relative units are:
| unit | relative to |
|---|---|
| em | font size of the element |
| ex | x-height of the element’s font |
| cap | cap height (the nominal height of capital letters) of the element’s font |
| ch | typical character advance of a narrow glyph in the element’s font, as represented by the “0” (ZERO, U+0030) glyph |
| ic | typical character advance of a fullwidth glyph in the element’s font, as represented by the “水” (CJK water ideograph, U+6C34) glyph |
| rem | font size of the root element |
| lh | line height of the element |
| rlh | line height of the root element |
| vw | 1% of viewport’s width |
| vh | 1% of viewport’s height |
| vi | 1% of viewport’s size in the root element’s inline axis |
| vb | 1% of viewport’s size in the root element’s block axis |
| vmin | 1% of viewport’s smaller dimension |
| vmax | 1% of viewport’s larger dimension |
Child elements do not inherit the relative values as specified for their parent; they inherit the computed values.
6.1.1. Font-relative Lengths: the em, rem, ex, rex, cap, rcap, ch, rch, ic, ric, lh, rlh units
The font-relative lengths refer to the font metrics either of the element on which they are used (for the local font-relative lengths) or of the root element (for the root font-relative lengths).
- em
- Equal to the computed value of the font-size property of the element on which it is used.
- rem
- Equal to the computed value of the em unit on the root element.
- ex
-
Equal to the used x-height of the first available font [CSS3-FONTS].
The x-height is so called because it is often equal to the height of the lowercase "x".
However, an ex is defined even for fonts that do not contain an "x".
The x-height of a font can be found in different ways.
Some fonts contain reliable metrics for the x-height.
If reliable font metrics are not available, UAs may determine the x-height from the height of a lowercase glyph.
One possible heuristic is to look at
how far the glyph for the lowercase "o" extends below the baseline,
and subtract that value from the top of its bounding box.
In the cases where it is impossible or impractical to determine the x-height,
a value of 0.5em must be assumed.
Tests
- ex-unit-001.html (live test) (source)
- ex-unit-002.html (live test) (source)
- ex-unit-003.html (live test) (source)
- numbers-units-007.xht (live test) (source)
- numbers-units-009.xht (live test) (source)
- numbers-units-010.xht (live test) (source)
- numbers-units-011.xht (live test) (source)
- numbers-units-012.xht (live test) (source)
- numbers-units-013.xht (live test) (source)
- numbers-units-015.xht (live test) (source)
- numbers-units-019.xht (live test) (source)
- units-001.xht (live test) (source)
- units-002.xht (live test) (source)
- units-003.xht (live test) (source)
- units-004.xht (live test) (source)
- units-005.xht (live test) (source)
- calc-ch-ex-lang.html (live test) (source)
- rex
- Equal to the value of the ex unit on the root element.
- cap
- Equal to the used cap-height of the first available font [CSS3-FONTS]. The cap-height is so called because it is approximately equal to the height of a capital Latin letter. However, a cap is defined even for fonts that do not contain Latin letters. The cap-height of a font can be found in different ways. Some fonts contain reliable metrics for the cap-height. If reliable font metrics are not available, UAs may determine the cap-height from the height of an uppercase glyph. One possible heuristic is to look at how far the glyph for the uppercase “O” extends below the baseline, and subtract that value from the top of its bounding box. In the cases where it is impossible or impractical to determine the cap-height, the font’s ascent must be used.
- rcap
- Equal to the value of the cap unit on the root element.
- ch
-
Represents the typical advance measure of European alphanumeric characters,
and measured as the used advance measure of the “0” (ZERO, U+0030) glyph
in the font used to render it.
(The advance measure of a glyph is its advance width or height,
whichever is in the inline axis of the element.)
Note: This measurement is an approximation (and in monospace fonts, an exact measure) of a single narrow glyph’s advance measure, thus allowing measurements based on an expected glyph count.
Note: The advance measure of a glyph depends on writing-mode and text-orientation as well as font settings, text-transform, and any other properties that affect glyph selection or orientation.
In the cases where it is impossible or impractical to determine the measure of the “0” glyph, it must be assumed to be 0.5em wide by 1em tall. Thus, the ch unit falls back to 0.5em in the general case, and to 1em when it would be typeset upright (i.e. writing-mode is vertical-rl or vertical-lr and text-orientation is upright).
Tests
- ch-unit-001.html (live test) (source)
- ch-unit-002.html (live test) (source)
- ch-unit-003.html (live test) (source)
- ch-unit-004.html (live test) (source)
- ch-unit-008.html (live test) (source)
- ch-unit-009.html (live test) (source)
- ch-unit-010.html (live test) (source)
- ch-unit-011.html (live test) (source)
- ch-unit-012.html (live test) (source)
- ch-unit-016.html (live test) (source)
- ch-unit-017.html (live test) (source)
- line-break-ch-unit.html (live test) (source)
- calc-ch-ex-lang.html (live test) (source)
- rch
- Equal to the value of the ch unit on the root element.
- ic
-
Represents the typical advance measure of CJK letters,
and measured as the used advance measure of the “水” (CJK water ideograph, U+6C34) glyph
found in the font used to render it.
Note: This measurement is a typically an exact measure (in the few fonts with proportional fullwidth glyphs, an approximation) of a single fullwidth glyph’s advance measure, thus allowing measurements based on an expected glyph count.
In the cases where it is impossible or impractical to determine the ideographic advance measure, it must be assumed to be 1em.
Tests
- ic-unit-001.html (live test) (source)
- ic-unit-002.html (live test) (source)
- ic-unit-003.html (live test) (source)
- ic-unit-004.html (live test) (source)
- ic-unit-008.html (live test) (source)
- ic-unit-009.html (live test) (source)
- ic-unit-010.html (live test) (source)
- ic-unit-011.html (live test) (source)
- ic-unit-012.html (live test) (source)
- ric
- Equal to the value of the ic unit on the root element.
- lh
- Equal to the computed value of the line-height property of the element on which it is used, converting normal to an absolute length by using only the metrics of the first available font.
- rlh
-
Equal to the value of the lh unit on the root element.
Note: Setting the height of an element using either the lh or the rlh units does not enable authors to control the actual number of lines in that element. These units only enable length calculations based on the theoretical size of an ideal empty line; the size of actual lines boxes may differ based on their content. In cases where an author wants to limit the number of actual lines in an element, the max-lines property can be used instead.
When used in the value of any font-* property on the element they refer to, the font-relative lengths resolve against the computed metrics of the parent element—or against the computed metrics corresponding to the initial values of the font and line-height properties, if the element has no parent. Similarly, when lh or rlh units are used in the value of the line-height property or font-* properties on the element they refer to, they resolve against the computed line-height and font metrics of the parent element—or the computed metrics corresponding to the initial values of the font and line-height properties, if the element has no parent. (The other font-relative lengths continue to resolve against the element’s own metrics when used in line-height.)
When used outside the context of an element (such as in media queries), the font-relative lengths units refer to the metrics corresponding to the initial values of the font and line-height properties. Similarly, when specified in a document with no root element, the root font-relative lengths are resolved assuming the initial values of the font and line-height properties.
Note: Font-relative units such as ch and ic can trigger font downloads, if a required font is not yet loaded.
The font-relative lengths are calculated in the absence of shaping.
Some user-agents allow users to apply additional restrictions to font sizes in a document, such as setting minimum font sizes to ensure readability. Such restrictions must be applied to the used value of the affected properties only; they must not affect the resolution of font-relative lengths used in properties. However, in other contexts (such as in media queries), to the extent that they would impact the used font metrics, such restrictions do affect the resolution of font-relative lengths.
Note: In general, respecting a user’s preferences, like minimum font sizes, is desirable; it’s useful for a media query like (min-width: 40em) to use the actual font size the document will be displayed in. However, having these preferences affect font-relative lengths in properties on an element was found to not be Web-compatible; too many pages expect these units to be exact multiples of the specified font-size, rather than the actual font-size after applying user preferences.
Some user-agents apply restrictions to the line-height values on form controls. These must have no effect on the lh and rlh units. The effect on their descendants, however, is implementation-defined.
6.1.2. Viewport-percentage Lengths: the *vw, *vh, *vi, *vb, *vmin, *vmax units
The viewport-percentage lengths are relative to the size of the initial containing block—which is itself based on the size of either the viewport (for continuous media) or the page area (for paged media). When the height or width of the initial containing block is changed, they are scaled accordingly.
6.1.2.1. The Large, Small, and Dynamic Viewport Sizes
There are four variants of the viewport-percentage length units, corresponding to three (possibly identical) notions of the viewport size.
- large viewport
-
The large viewport-percentage units (lv*)
and default viewport-percentage units (v*)
are defined with respect to the large viewport size:
the viewport sized assuming
any UA interfaces that are dynamically expanded and retracted
to be retracted.
This allows authors to size content
such that it is guaranteed to fill the viewport,
noting that such content might be hidden behind such interfaces
when they are expanded.
The sizes of the large viewport-percentage units are fixed (and therefore stable) unless the viewport itself is resized.
For example, on phones, where screen real-estate is at a premium, browsers will often hide part or all of the title and address bar once the user starts scrolling the page. The large viewport-percentage units are sized relative to this larger everything-retracted space, so content using these units will fill the entire visible page when these UI elements are hidden. However, when these retractable elements are shown, they can obscure content that is sized or positioned using these units. - small viewport
-
The small viewport-percentage units (sv*)
are defined with respect to the small viewport size:
the viewport sized assuming
any UA interfaces that are dynamically expanded and retracted
to be expanded.
This allows authors to size content
such that it can fit within the viewport
even when such interfaces are present,
noting that such content might not fill the viewport
when such interfaces are retracted.
The sizes of the small viewport-percentage units are fixed (and therefore stable) unless the viewport itself is resized.
An element that is sized as height: 100svh, for example, will fill the screen perfectly, without any of its content being obscured, when all the dynamic UI elements of the UA are shown.Once those UI elements start being hidden, however, there will be extra space around the element. The small viewport-percentage units units are thus “safer” in general, but might not produce the most attractive layout once the user starts interacting with the page.
- dynamic viewport
-
The dynamic viewport-percentage units (dv*)
are defined with respect to the dynamic viewport size:
the viewport sized
with dynamic consideration of any UA interfaces
that are dynamically expanded and retracted.
This allows authors to size content
such that it can exactly fit within the viewport
whether or not such interfaces are present.
The sizes of the dynamic viewport-percentage units are not stable even while the viewport itself is unchanged. Using these units can cause content to resize e.g. while the user scrolls the page. Depending on usage, this can be disturbing to the user and/or costly in terms of performance.
The UA is not required to animate the dynamic viewport-percentage units while expanding and retracting any relevant interfaces, and may instead calculate the units as if the relevant interface was fully expanded or retracted during the UI animation. (It is recommended that UAs assume the fully-retracted size for this duration.)
Whether the expansion/retraction of a particular interface (A) changes the sizes of all of the viewport-percentage lengths (and the initial containing block) simultaneously or (B) contributes to the differences between the large viewport size and small viewport size is largely UA-dependent. However:
-
Changes in interface that happen as a result of scrolling or other frequent page interactions that would disturb the user if they resulted in substantial layout changes must be categorized as the latter (B).
-
Changes in interface that have a sufficiently steady state that re-laying out the document into the adjusted space would be beneficial to the user must be categorized as the former (A).
-
Additionally, UAs may have some dynamically-shown interfaces that intentionally overlay content and do not cause any shifts in layout—and therefore have no effect on any of the viewport-percentage lengths. (Typically on-screen keyboards will fit into this category.)
In all cases, if the value of overflow or scrollbar-gutter on the root element in either axis would cause scrollbars to appear (or space to be reserved for them) unconditionally (for example, overflow: scroll, but not overflow: auto), the computed values of the viewport-percentage lengths in that axis are reduced in accordance with the initial containing block. Otherwise, and always in the case of media queries, the viewport-percentage lengths are sized assuming that scrollbars do not exist (even if this diverges from the initial containing block).
Note: The value of overflow on the body element can sometimes affect the presence of scrollbars on the root element. This does not affect the size of viewport units, however.
6.1.2.2. The Various Viewport-relative Units
The viewport-percentage length units are:
- vw
- svw
- lvw
- dvw
- svw
- Equal to 1% of the width of the large viewport size, small viewport size, large viewport size, and dynamic viewport size, respectively.
- vh
- svh
- lvh
- dvh
- svh
- Equal to 1% of the height of the large viewport size, small viewport size, large viewport size, and dynamic viewport size, respectively.
- vi
- svi
- lvi
- dvi
- svi
- Equal to 1% of the size of the large viewport size, small viewport size, large viewport size, and dynamic viewport size (respectively) in the box’s inline axis.
- vb
- svb
- lvb
- dvb
- svb
- Equal to 1% of the size of the initial containing block large viewport size, small viewport size, large viewport size, and dynamic viewport size (respectively) in the box’s block axis.
- vmin
- svmin
- lvmin
- dvmin
- svmin
- Equal to the smaller of *vw or *vh.
- vmax
- svmax
- lvmax
- dvmax
- svmax
- Equal to the larger of *vw or *vh.
Tests
- vh-calc-support-pct.html (live test) (source)
- vh-calc-support.html (live test) (source)
- vh-em-inherit.html (live test) (source)
- vh-inherit.html (live test) (source)
- vh-interpolate-pct.html (live test) (source)
- vh-interpolate-px.html (live test) (source)
- vh-interpolate-vh.html (live test) (source)
- vh-support.html (live test) (source)
- vh-support-margin.html (live test) (source)
- vh-support-transform-origin.html (live test) (source)
- vh-support-transform-translate.html (live test) (source)
- vh-zero-support.html (live test) (source)
- vh_not_refreshing_on_chrome.html (live test) (source)
- viewport-relative-lengths-scaled-viewport.html (live test) (source)
- viewport-unit-011.html (live test) (source)
- viewport-units-css2-001.html (live test) (source)
Note: The original (unprefixed) viewport units were defined relative to the initial containing block, which in continuous media always matched the (singular) viewport size. The dynamism of browser chrome shifting in and out during scrolling was invented later, and following Safari’s lead, most UAs mapped these units to the larger size. Defining it this way is prettier in many cases, but can also block critical content (such as toolbars, headers, and footers) in others. It’s therefore not entirely clear whether this was the best mapping, and thus earlier editions of this specifications allowed UAs to choose the mapping of these default units. However at this point the mapping to the large viewport-percentage units is presumed to be required for Web compatibility.
In situations where there is no element or it hasn’t yet been styled (such as when evaluating media queries), the *vi and *vb units use the initial value of the writing-mode property to determine which axis they correspond to.
6.2. Absolute Lengths: the cm, mm, Q, in, pt, pc, px units
The absolute length units are fixed in relation to each other and anchored to some physical measurement. They are mainly useful when the output environment is known. The absolute units consist of the physical units (in, cm, mm, pt, pc, Q) and the visual angle unit (pixel unit) (px):
| unit | name | equivalence |
|---|---|---|
| cm | centimeters | 1cm = 96px/2.54 |
| mm | millimeters | 1mm = 1/10th of 1cm |
| Q | quarter-millimeters | 1Q = 1/40th of 1cm |
| in | inches | 1in = 2.54cm = 96px |
| pc | picas | 1pc = 1/6th of 1in |
| pt | points | 1pt = 1/72nd of 1in |
| px | pixels | 1px = 1/96th of 1in |
h1{ margin : 0.5 in } /* inches */ h2{ line-height : 3 cm } /* centimeters */ h3{ word-spacing : 4 mm } /* millimeters */ h3{ letter-spacing : 1 Q } /* quarter-millimeters */ h4{ font-size : 12 pt } /* points */ h4{ font-size : 1 pc } /* picas */ p{ font-size : 12 px } /* px */
Note: Lengths in publishing contexts
are sometimes written like
All of the absolute length units are compatible, and px is their canonical unit.
For a CSS device, these dimensions are anchored either
- by relating the physical units to their physical measurements, or
- by relating the pixel unit to the reference pixel.
For print media at typical viewing distances, the anchor unit should be one of the physical units (inches, centimeters, etc). For screen media (including high-resolution devices), low-resolution devices, and devices with unusual viewing distances, it is recommended instead that the anchor unit be the pixel unit. For such devices it is recommended that the pixel unit refer to the whole number of device pixels that best approximates the reference pixel.
Note: If the anchor unit is the pixel unit, the physical units might not match their physical measurements. Alternatively if the anchor unit is a physical unit, the pixel unit might not map to a whole number of device pixels.
Note: This definition of the pixel unit and the physical units differs from the earlier editions of CSS1 and CSS2. In particular, in previous versions of CSS the pixel unit and the physical units were not related by a fixed ratio: the physical units were always tied to their physical measurements while the pixel unit would vary to most closely match the reference pixel. (This unfortunate change was made because too much existing content relies on the assumption of 96dpi, and breaking that assumption broke the content.)
Note: Units are ASCII case-insensitive and serialize as lowercase, for example 1Q serializes as 1q.
Tests
- absolute-length-units-001.html (live test) (source)
- q-unit-case-insensitivity-001.html (live test) (source)
- q-unit-case-insensitivity-002.html (live test) (source)
- units-001.xht (live test) (source)
- units-006.xht (live test) (source)
- units-008.xht (live test) (source)
- units-009.xht (live test) (source)
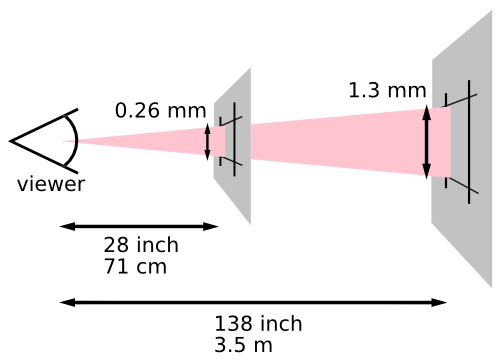
The reference pixel is the visual angle of one pixel on a device with a device pixel density of 96dpi and a distance from the reader of an arm’s length. For a nominal arm’s length of 28 inches, the visual angle is therefore about 0.0213 degrees. For reading at arm’s length, 1px thus corresponds to about 0.26 mm (1/96 inch).
The image below illustrates the effect of viewing distance on the size of a reference pixel: a reading distance of 71 cm (28 inches) results in a reference pixel of 0.26 mm, while a reading distance of 3.5 m (12 feet) results in a reference pixel of 1.3 mm.
This second image illustrates the effect of a device’s resolution on the pixel unit: an area of 1px by 1px is covered by a single dot in a low-resolution device (e.g. a typical computer display), while the same area is covered by 16 dots in a higher resolution device (such as a printer).
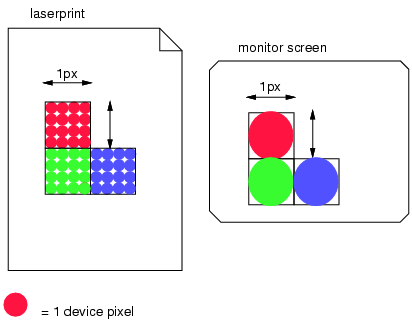
A device pixel is the smallest unit of area on the device output capable of displaying its full range of colors. For typical color screens, it’s a square or somewhat rectangular region containing a red, green, and blue subpixel. Many non-traditional outputs exist that can blur this definition, such as by displaying some colors at higher resolutions. Such devices still expose some equivalent notion of "device pixel", however.
7. Other Quantities
7.1. Angle Units: the <angle> type and deg, grad, rad, turn units
Angle values are <dimension>s denoted by <angle>. The angle unit identifiers are:
- deg
- Degrees. There are 360 degrees in a full circle.
- grad
- Gradians, also known as "gons" or "grades". There are 400 gradians in a full circle.
- rad
- Radians. There are 2π radians in a full circle.
- turn
- Turns. There is 1 turn in a full circle.
For example, a right angle is 90deg or 100grad or 0.25turn or approximately 1.57rad.
All <angle> units are compatible, and deg is their canonical unit.
For example, in the linear-gradient() function, the <angle> that determines the direction of the gradient is interpreted as a bearing angle.
Note: For legacy reasons, some uses of <angle> allow a bare 0 to mean 0deg. This is not true in general, however, and will not occur in future uses of the <angle> type.
Tests
7.2. Duration Units: the <time> type and s, ms units
Time values are dimensions denoted by <time>. The time unit identifiers are:
- s
- Seconds.
- ms
- Milliseconds. There are 1000 milliseconds in a second.
All <time> units are compatible, and s is their canonical unit.
Properties may restrict the time value to some range. If the value is outside the allowed range, the declaration is invalid and must be ignored.
Tests
7.3. Frequency Units: the <frequency> type and Hz, kHz units
Frequency values are dimensions denoted by <frequency>. The frequency unit identifiers are:
- Hz
- Hertz. It represents the number of occurrences per second.
- kHz
- KiloHertz. A kiloHertz is 1000 Hertz.
For example, when representing sound pitches, 200Hz (or 200hz) is a bass sound, and 6kHz (or 6khz) is a treble sound.
All <frequency> units are compatible, and hz is their canonical unit.
Note: Units are ASCII case-insensitive and serialize as lowercase, for example 1Hz serializes as 1hz.
7.4. Resolution Units: the <resolution> type and dpi, dpcm, dppx units
Resolution units are dimensions denoted by <resolution>. The resolution unit identifiers are:
- dpi
- Dots per inch.
- dpcm
- Dots per centimeter.
- dppx
- x
- Dots per px unit.
The <resolution> unit represents the size of a single "dot" in a graphical representation by indicating how many of these dots fit in a CSS in, cm, or px. For uses, see e.g. the resolution media query in [MEDIAQ] or the image-resolution property defined in [CSS3-IMAGES].
All <resolution> units are compatible, and dppx is their canonical unit.
The allowed range of <resolution> values always excludes negative values, in addition to any explicit ranges that might be specified.
Note that due to the 1:96 fixed ratio of CSS in to CSS px, 1dppx is equivalent to 96dpi. This corresponds to the default resolution of images displayed in CSS: see image-resolution.
@media ( min-resolution:2 dppx ) { ...}
8. Data Types Defined Elsewhere
Some data types are defined in their own modules. This example talks about some of the most common ones used across several specifications.
8.1. Colors: the <color> type
The <color> data type is defined in [CSS-COLOR-4]. UAs must interpret <color> as defined therein.
8.1.1. Combination of <color>
Interpolation of <color> is defined in CSS Color 4 § 12. Color Interpolation. Interpolation is done between premultiplied colors, as defined in CSS Color 4 § 12.3 Interpolating with Alpha.
The <color> type is not additive.
Note: the CSS WG is interested to hear use-cases for addition of <color>, and may consider making <color> additive in the future.
8.2. Images: the <image> type
The <image> data type is defined in [CSS3-IMAGES]. UAs that support CSS Images Level 3 or its successor must interpret <image> as defined therein. UAs that do not yet support CSS Images Level 3 must interpret <image> as <url>.
8.2.1. Combination of <image>
Note: Interpolation of <image> is defined in CSS Images 3 § 6 Interpolation.
Images are not additive.
8.3. 2D Positioning: the <position> type
The <position> value specifies the position of a object area (e.g. background image) inside a positioning area (e.g. background positioning area). It is computed and interpreted as specified for background-position. [CSS3-BACKGROUND]
<position> =[ [ left | center | right | top | bottom | <length-percentage>] |[ left | center | right] &&[ top | center | bottom] |[ left | center | right | <length-percentage>] [ top | center | bottom | <length-percentage>] |[ [ left | right] <length-percentage>] &&[ [ top | bottom] <length-percentage>] ]
Note: The background-position property also accepts a three-value syntax. This has been disallowed generically because it creates parsing ambiguities when combined with other length or percentage components in a property value.
8.3.1. Parsing <position>
When specified in a grammar alongside other keywords, <length>s, or <percentage>s, <position> is greedily parsed; it consumes as many components as possible.
8.3.2. Serializing <position>
When serializing the specified value of a <position>:
- If only one component is specified:
-
-
The implied center keyword is added, and a 2-component value is serialized.
-
- If two components are specified:
-
-
Keywords are serialized as keywords.
-
<length-percentage>s are serialized as <length-percentage>s.
-
Components are serialized horizontal first, then vertical.
-
- If four components are specified:
-
-
Keywords and offsets are both serialized.
-
Components are serialized horizontal first, then vertical.
-
Note: <position> values are never serialized as a single value, even when a single value would produce the same behavior, to avoid causing parsing ambiguities in some grammars where a <position> is placed next to a <length>, such as transform-origin.
Note: Computed values are always serialized as two offsets (without keywords) because the computed value does not preserve syntactic distinctions.
8.3.3. Combination of <position>
Interpolation of <position> is defined as the independent interpolation of each component (x, y) normalized as an offset from the top left corner as a <length-percentage>.
Addition of <position> is likewise defined as the independent addition each component (x, y) normalized as an offset from the top left corner as a <length-percentage>.
9. Functional Notations
A functional notation is a type of component value that can represent more complex types or invoke special processing. The syntax starts with the name of the function immediately followed by a left parenthesis (i.e. a <function-token>) followed by the argument(s) to the notation followed by a right parenthesis. Like keywords, function names are ASCII case-insensitive. White space is allowed, but optional, immediately inside the parentheses. Functions can take multiple arguments, which are formatted similarly to a CSS property value. See § 2.6 Functional Notation Definitions.
Note: Some legacy functional notations, such as rgba(), use commas unnecessarily, but generally commas are only used to separate items in a list, or pieces of a grammar that would be ambiguous otherwise. If a comma is used to separate arguments, white space is optional before and after the comma.
background : url ( http://www.example.org/image ); color : rgb ( 100 , 200 , 50 ); content : counter ( list-item) ". " ; width : calc ( 50 % -2 em );
The math functions are defined below. Other functional notations are defined in their own modules; for example the <color> functions are defined in [CSS-COLOR-4] and [CSS-COLOR-5].
10. Mathematical Expressions
The math functions (calc(), clamp(), sin(), and others defined in this chapter) allow numeric CSS values to be written as mathematical expressions.
A math function represents a numeric value, one of:
...or the <length-percentage>/etc mixed types, and can be used wherever such a value would be valid.
10.1. Basic Arithmetic: calc()
The calc() function is a math function that allows basic arithmetic to be performed on numerical values, using addition (+), subtraction (-), multiplication (*), division (/), and parentheses.
A calc() function contains a single calculation, which is a sequence of values interspersed with operators, and possibly grouped by parentheses (matching the <calc-sum> grammar), which represents the result of evaluating the expression using standard operator precedence rules (* and / bind tighter than + and -, and operators are otherwise evaluated left-to-right). The calc() function represents the result of its contained calculation.
Components of a calculation can be literal values (such as 5px), other math functions, or other expressions, such as var(), that evaluate to a valid argument type (like <length>).
Math functions can be used to combine value that use different units. In this example the author wants the margin box of each section to take up 1/3 of the space, so they start with 100%/3, then subtract the element’s borders and margins. (box-sizing can automatically achieve this effect for borders and padding, but a math function is needed if you want to include margins.)
section{ float : left; margin : 1 em ; border : solid1 px ; width : calc ( 100 % /3 -2 *1 em -2 *1 px ); }
Similarly, in this example the gradient will show a color transition only in the first and last 20px of the element:
.fade{ background-image : linear-gradient ( silver0 % , white20 px , whitecalc ( 100 % -20 px ), silver100 % ); }
Math functions can also be useful just to express values in a more natural, readable fashion, rather than as an obscure decimal. For example, the following sets the font-size so that exactly 35em fits within the viewport, ensuring that roughly the same amount of text always fills the screen no matter the screen size.
:root{ font-size : calc ( 100 vw /35 ); }
Functionality-wise, this is identical to just writing font-size: 2.857vw, but then the intent (that 35em fills the viewport) is much less clear to someone reading the code; the later reader will have to reverse the math themselves to figure out that 2.857 is meant to approximate 100/35.
Standard mathematical precedence rules for the operators apply: calc(2 + 3 * 4) is equal to 14, not 20.
Parentheses can be used to manipulate precedence: calc((2 + 3) * 4) is instead equal to 20.
Parentheses and nesting additional calc() functions are equivalent; the preceding expression could equivalently have been written as calc(calc(2 + 3) * 4). This can be useful when building up values piecemeal via var(), such as in the following example:
.aspect-ratio-box{ --ar : calc ( 16 /9 ); --w : calc ( 100 % /3 ); --h : calc ( var ( --w) /var ( --ar)); width : var ( --w); height : var ( --h); }
Although --ar could have been written as simply --ar: (16 / 9);, --w is used both on its own (in width) and as a calc() component (in --h), so it has to be written as a full calc() function itself.
Tests
10.2. Comparison Functions: min(), max(), and clamp()
The comparison functions of min(), max(), and clamp() compare multiple calculations and represent the value of one of them.
The min() or max() functions contain one or more comma-separated calculations, and represent the smallest (most negative) or largest (most positive) of them, respectively.
The clamp() function takes three calculations—a minimum value, a central value, and a maximum value—and represents its central calculation, clamped according to its min and max calculations, favoring the min calculation if it conflicts with the max. (That is, given clamp(MIN, VAL, MAX), it represents exactly the same value as max(MIN, min(VAL, MAX))).
Either the min or max calculations (or even both) can instead be the keyword none, which indicates the value is not clamped from that side. (That is, clamp(MIN, VAL, none) is equivalent to max(MIN, VAL), clamp(none, VAL, MAX) is equivalent to min(VAL, MAX), and clamp(none, VAL, none) is equivalent to just calc(VAL).)
For all three functions, the argument calculations can resolve to any <number>, <dimension>, or <percentage>, but must have a consistent type or else the function is invalid; the result’s type will be the consistent type.
min(), max(), and clamp() can be used to make sure a value doesn’t exceed a "safe" limit: For example, "responsive type" that sets font-size with viewport units might still want a minimum size to ensure readability:
.type{ /* Set font-size to 10x the average of vw and vh, but don’t let it go below 12px. */ font-size:max ( 10 *( 1 vw +1 vh ) /2 , 12 px ); }
Note: Full math expressions are allowed in each of the arguments; there’s no need to nest a calc() inside! You can also provide more than two arguments, if you have multiple constraints to apply.
.type{ /* Force the font-size to stay between 12px and 100px */ font-size:clamp ( 12 px , 10 *( 1 vw +1 vh ) /2 , 100 px ); }
Or, if you only wanted to impose a minimum size, but allow the font-size to grow as large as it wants:
.type{ /* Force the font-size to be at least 12px */ font-size:clamp ( 12 px , 10 *( 1 vw +1 vh ) /2 , none); }
If alternate resolution mechanics are desired they can be achieved by combining clamp() with min() or max():
- To have MAX win over MIN:
-
clamp(min(MIN, MAX), VAL, MAX). If you want to avoid repeating the MAX calculation, you can just reverse the nesting of functions that clamp() is defined against—min(MAX, max(MIN, VAL)).
- To have MAX and MIN "swap" when they’re in the wrong order:
-
clamp(min(MIN, MAX), VAL, max(MIN, MAX)). Unfortunately, there’s no easy way to do this without repeating the MIN and MAX terms.
10.3. Stepped Value Functions: round(), mod(), and rem()
The stepped-value functions, round(), mod(), and rem(), all transform a given value according to another "step value", in different ways.
The round(<rounding-strategy>?, A, B?) function contains an optional rounding strategy, and two calculations A and B, and returns the value of A, rounded according to the rounding strategy, to the nearest integer multiple of B either above or below A. The argument calculations can resolve to any <number>, <dimension>, or <percentage>, but must have a consistent type or else the function is invalid; the result’s type will be the consistent type.
If A is exactly equal to an integer multiple of B, round() resolves to A exactly (preserving whether A is 0⁻ or 0⁺, if relevant). Otherwise, there are two integer multiples of B that are potentially "closest" to A, lower B which is closer to −∞ and upper B which is closer to +∞. The following <rounding-strategy>s dictate how to choose between them:
- nearest
-
Choose whichever of lower B and upper B that has the smallest absolute difference from A. If both have an equal difference (A is exactly between the two values), choose upper B.
- up
-
Choose upper B.
- down
-
Choose lower B.
- to-zero
-
Choose whichever of lower B and upper B that has the smallest absolute difference from 0.
If lower B would be zero, it is specifically equal to 0⁺; if upper B would be zero, it is specifically equal to 0⁻.
If <rounding-strategy> is omitted, it defaults to nearest. (Aka rounding to the nearest integer.) If the type of A matches <number>, then B may be omitted, and defaults to 1; omitting B is otherwise invalid.
CSSOM needs to specify how it rounds, and it’s probably good for CSS functions to round the same way by default. What behavior should be used? [Issue #5689]
Note: JavaScript and other programming languages
sometimes separate out the rounding strategies into separate rounding functions.
JS’s Math is equivalent to CSS’s round(down, ...);
JS’s Math is equivalent to CSS’s round(up, ...);
JS’s Math is equivalent to CSS’s round(to-zero, ...);
and JS’s Math is equivalent to CSS’s round(nearest, ...),
or just round(...).
Note: The <rounding-strategy> keywords are the same as the keywords in block-step-size and have the same behavior. (block-step-size just lacks to-zero; since block sizes are always non-negative, to-zero and down would be identical.)
The modulus functions mod(A, B) and rem(A, B) similarly contain two calculations A and B, and return the difference between A and the nearest integer multiple of B either above or below A. The argument calculations can resolve to any <number>, <dimension>, or <percentage>, but must have the same type, or else the function is invalid; the result will have the same type as the arguments.
The two functions are very similar, and in fact return identical results if both arguments are positive or both are negative: the value of the function is equal to the value of A shifted by the integer multiple of B that brings the value between zero and B. (Specifically, the range includes zero and excludes B. More specifically, if B is positive the range starts at 0⁺, and if B is negative it starts at 0⁻.)
Similarly, mod(-140deg, -90deg) resolves to the value -50deg, because adding -90deg * 1 to -140deg yields -50deg, which is the only such value between 0deg and -90deg.
Evaluating either of these examples with rem() yields the exact same results.
Their behavior diverges if the A value and the B step are on opposite sides of zero: mod() (short for “modulus”) continues to choose the integer multiple of B that puts the value between zero and B, as above (guaranteeing that the result will either be zero or share the sign of B, not A), while rem() (short for "remainder") chooses the integer multiple of B that puts the value between zero and -B, avoiding changing the sign of the value.
On the other hand, rem(-18px, 5px) resolves to the value -3px: adding 5px * 3 to -18px yields -3px, which has the same sign as -18px but is between 0px and -5px.
Similarly, mod(140deg, -90deg) resolves to the value -40deg (adding -90deg * 2 to 140deg, bringing it to between 0deg and -90deg), but rem(140deg, -90deg) resolves to the value 50deg.
When should I choose mod() vs rem()?
Typically, users of this operation are in control of the step value (B), and are modifying an unknown value A. As a result, it’s usually more expected that the result is between 0 and B, regardless of A’s sign, meaning mod() should be chosen.
For example, if an author wants to know whether a length is an even or odd number of pixels, mod(A, 2px) will return either 0px or 1px (assuming the value is a whole number of pixels to begin with), regardless of the value of a. rem(A, 2px), on the other hand, will return 0px if A is an even number of pixels, but will return either 1px or -1px if it’s odd, depending on whether A is positive or negative.
The opposite situation does sometimes occur,
however,
and so rem() is provided to cater to that.
As well, rem() is the behavior of JavaScript’s
Note: mod() and rem() can also be defined directly in terms of other functions: mod(A, B) is equivalent to calc(A - sign(B)*round(down, A*sign(B), B)) (a hacky way to say "round(down) when B is positive, round(up) when B is negative), while rem(A, B) is equivalent to calc(A - round(to-zero, A, B)). (These expressions don’t always handle 0⁺ and 0⁻ correctly, though, because 0⁻ semantics aren’t commutative for addition.)
10.3.1. Argument Ranges
In round(A, B), if B is 0, the result is NaN. If A and B are both infinite, the result is NaN.
If A is infinite but B is finite, the result is the same infinity.
If A is finite but B is infinite, the result depends on the <rounding-strategy> and the sign of A:
- nearest
- to-zero
-
If A is positive or 0⁺, return 0⁺. Otherwise, return 0⁻.
- up
-
If A is positive (not zero), return +∞. If A is 0⁺, return 0⁺. Otherwise, return 0⁻.
- down
-
If A is negative (not zero), return −∞. If A is 0⁻, return 0⁻. Otherwise, return 0⁺.
In mod(A, B) or rem(A, B), if B is 0, the result is NaN. If A is infinite, the result is NaN.
In mod(A, B) only, if B is infinite and A has opposite sign to B (including an oppositely-signed zero), the result is NaN.
Note: All other "infinite B" cases are valid, and just return A immediately.
10.4. Trigonometric Functions: sin(), cos(), tan(), asin(), acos(), atan(), and atan2()
The trigonometric functions—sin(), cos(), tan(), asin(), acos(), atan(), and atan2()—compute the various basic trigonometric relationships.
The sin(A), cos(A), and tan(A) functions all contain a single calculation which must resolve to either a <number> or an <angle>, and compute their corresponding function by interpreting the result of their argument as radians. (That is, sin(45deg), sin(.125turn), and sin(3.14159 / 4) all represent the same value, approximately .707.) They all represent a <number>, with the return type made consistent with the input calculation’s type. sin() and cos() will always return a number between −1 and 1, while tan() can return any number between −∞ and +∞. (See § 10.9 Type Checking for details on how math functions handle ∞.)
The asin(A), acos(A), and atan(A) functions are the "arc" or "inverse" trigonometric functions, representing the inverse function to their corresponding "normal" trig functions. All of them contain a single calculation which must resolve to a <number>, and compute their corresponding function, interpreting their result as a number of radians, representing an <angle> with the return type made consistent with the input calculation’s type. The angle returned by asin() must be normalized to the range [-90deg, 90deg]; the angle returned by acos() to the range [0deg, 180deg]; and the angle returned by atan() to the range [-90deg, 90deg].
The atan2(A, B) function contains two comma-separated calculations, A and B. A and B can resolve to any <number>, <dimension>, or <percentage>, but must have a consistent type or else the function is invalid. The function returns the <angle> between the positive X-axis and the point (B,A), with the return type made consistent with the input calculation’s type. The returned angle must be normalized to the interval (-180deg, 180deg] (that is, greater than -180deg, and less than or equal to 180deg).
Note: atan2(Y, X) is generally equivalent to atan(Y / X), but it gives a better answer when the point in question may include negative components. atan2(1, -1), corresponding to the point (-1, 1), returns 135deg, distinct from atan2(-1, 1), corresponding to the point (1, -1), which returns -45deg. In contrast, atan(1 / -1) and atan(-1 / 1) both return-45deg, because the internal calculation resolves to -1 for both.
10.4.1. Argument Ranges
In sin(A), cos(A), or tan(A), if A is infinite, the result is NaN. (See § 10.9 Type Checking for details on how math functions handle NaN.)
In sin(A) or tan(A), if A is 0⁻, the result is 0⁻.
In tan(A), if A is one of the asymptote values
(such as 90deg, 270deg, etc),
the numeric result is implementation-defined.
If an implementation is capable of exactly representing these inputs,
it should return
+∞ for the asymptotes at
Why are these implementation-defined?
The tangent function is discontinuous at its asymptotes: it approaches infinity from one side and negative infinity from the other side, and isn’t defined at the exact values of the asymptote.
Further, whether or not the asymptotic values are exactly representable in implementations depends on how they internally store and manipulate angles; when written in degrees the values are simple (90deg, etc), but in radians the values are transcendental (pi / 2, etc) and cannot be exactly represented. So, even defining a specific behavior for these values is difficult; if an implementation uses radians internally, it would have to do some fuzzy matching to return the defined value when the input is sufficiently close to the asymptote.
The other major language for the Web, JavaScript, exposes these functions as taking radians only, so it can’t hit the exact asymptotes either (and this true for most other computer languages, too). Authors writing code in JS, then, can’t rely on any specific behavior for these values either, and it’s unlikely that their needs in CSS are significantly different.
The suggested behavior for implementations that can exactly represent the asymptote values preserves round-tripping with the atan() function: tan(atan(X)) and atan(tan(X)) will both return (approximately) X for all possible X values, given this definition. It also means that within the supported output range of atan(), the function is continuous.
In asin(A) or acos(A), if A is less than -1 or greater than 1, the result is NaN.
In acos(A), if A is exactly 1, the result is 0.
In asin(A) or atan(A), if A is 0⁻, the result is 0⁻.
In atan(A), if A is +∞, the result is 90deg; if A is −∞, the result is -90deg.
In atan2(Y, X), the following table gives the results for all unusual argument combinations:
| X | |||||||
|---|---|---|---|---|---|---|---|
| −∞ | -finite | 0⁻ | 0⁺ | +finite | +∞ | ||
| Y | −∞ | -135deg | -90deg | -90deg | -90deg | -90deg | -45deg |
| -finite | -180deg | (normal) | -90deg | -90deg | (normal) | 0⁻deg | |
| 0⁻ | -180deg | -180deg | -180deg | 0⁻deg | 0⁻deg | 0⁻deg | |
| 0⁺ | 180deg | 180deg | 180deg | 0⁺deg | 0⁺deg | 0⁺deg | |
| +finite | 180deg | (normal) | 90deg | 90deg | (normal) | 0⁺deg | |
| +∞ | 135deg | 90deg | 90deg | 90deg | 90deg | 45deg | |
Note: All of these behaviors are intended to match the "standard" definitions of these functions as implemented by most programming languages, in particular as implemented in JS.
10.5. Exponential Functions: pow(), sqrt(), hypot(), log(), exp()
The exponential functions—pow(), sqrt(), hypot(), log(), and exp()—compute various exponential functions with their arguments.
The pow(A, B) function contains two comma-separated calculations A and B, both of which must resolve to <number>s, and returns the result of raising A to the power of B, returning the value as a <number>. The input calculations must have a consistent type or else the function is invalid; the result’s type will be the consistent type.
The sqrt(A) function contains a single calculation which must resolve to a <number>, and returns the square root of the value as a <number>, with the return type made consistent with the input calculation’s type. (sqrt(X) and pow(X, .5) are basically equivalent, differing only in some error-handling; sqrt() is a common enough function that it is provided as a convenience.)
The hypot(A, …) function contains one or more comma-separated calculations, and returns the length of an N-dimensional vector with components equal to each of the calculations. (That is, the square root of the sum of the squares of its arguments.) The argument calculations can resolve to any <number>, <dimension>, or <percentage>, but must have a consistent type or else the function is invalid; the result’s type will be the consistent type.
Why does hypot() allow dimensions (values with units), but pow() and sqrt() only work on numbers?
You are allowed to write expressions like hypot(30px, 40px), which resolves to 50px, but you aren’t allowed to write the expression sqrt(pow(30px, 2) + pow(40px, 2)), despite the two being equivalent in most mathematical systems.
There are two reasons for this: numeric precision in the exponents, and clashing expectations from authors.
First, numerical precision. For a type to match a CSS production like <length>, it needs to have a single unit with its exponent set to exactly 1. Theoretically, expressions like pow(pow(30px, 3), 1/3) should result in exactly that: the inner pow(30px, 3) would resolve to a value of 27000 with a type of «[ "length" → 3 ]» (aka <length>³), and then the pow(X, 1/3) would cube-root the value back down to 30 and multiply the exponent by 1/3, giving «[ "length" → 1 ]», which matches <length>.
In the realm of pure mathematics, that’s guaranteed to work out;
in the real-world of computers using binary floating-point arithmetic,
in some cases the powers might not exactly cancel out,
leaving you with an invalid math function for confusing, hard-to-track-down reasons.
(For a JS example,
evaluate Math.;
the result is not exactly 30,
because
Requiring authors to cast their value down into a number, do all the math on the raw number, then finally send it back to the desired unit, while inconvenient, ensures that numerical precision won’t bite anyone: calc(pow(pow(30px / 1px, 3), 1/3) * 1px) is guaranteed to resolve to a <length>, with a value that, if not exactly 30, is at least very close to 30, even if numerical precision actually prevents the powers from exactly canceling.
Second, clashing expectations. It’s not uncommon for authors to expect pow(30px, 2) to result in 900px (such as in this Sass issue); that is, just squaring the numerical value and leaving the unit alone. This, however, means the result is dependent on what unit you’re expressing the argument in; if 1em is 16px, then pow(1em, 2) would give 1em, while pow(16px, 2) would give 256px, or 16em, which are very different values for what should otherwise be identical input arguments! This sort of input dependency is troublesome for CSS, which generally allows values to be canonicalized freely; it also makes more complex expressions like pow(2em + 10px, 2) difficult to interpret.
Again, requiring authors to cast their value down into a number and then back up again into the desired unit sidesteps these issues; pow(30, 2) is indeed 900, and the author can interpret that however they wish.
On the other hand, hypot() doesn’t suffer from these problems. Numerical precision in units isn’t a concern, as the inputs and output all have the same type. The result isn’t unit-dependent, either, due to the nature of the operation; hypot(3em, 4em) and hypot(48px, 64px) both result in the same length when 1em equals 16px: 5em or 80px. Thus it’s fine to let author use dimensions directly in hypot().
The log(A, B?) function contains one or two calculations (representing the value to be logarithmed, and the base of the logarithm, defaulting to e), which must resolve to <number>s, and returns the logarithm base B of the value A, as a <number> with the return type made consistent with the input calculation’s type.
The exp(A) function contains one calculation which must resolve to a <number>, and returns the same value as pow(e, A) as a <number> with the return type made consistent with the input calculation’s type.
These sizes can be easily written into custom properties like:
:root{ --h6 : calc ( 1 rem *pow ( 1.5 , -1 )); --h5 : calc ( 1 rem *pow ( 1.5 , 0 )); --h4 : calc ( 1 rem *pow ( 1.5 , 1 )); --h3 : calc ( 1 rem *pow ( 1.5 , 2 )); --h2 : calc ( 1 rem *pow ( 1.5 , 3 )); --h1 : calc ( 1 rem *pow ( 1.5 , 4 )); }
...rather than writing out the values in pre-calculated numbers like 5.0625rem (what calc(1rem * pow(1.5, 4)) resolves to) which have less clear provenance when encountered in a stylesheet.
With more arguments, it gives the size of the main diagonal of a box whose side lengths are given by the arguments. This can be useful for transform-related things, giving the distance that an element will actually travel when it’s translated by a particular X, Y, and Z amount.
For example, hypot(30px, 40px) resolves to 50px, which is indeed the distance between an element’s starting and ending positions when it’s translated by a translate(30px, 40px) transform. If an author wanted elements to get smaller as they moved further away from their starting point (drawing some sort of word cloud, for example), they could then use this distance in their scaling factor calculations.
If one instead wants log base 10 (to, for example, count the number of digits in a value) or log base 2 (counting the number of bits in a value), log(X, 10) or log(X, 2) provide those values.
10.5.1. Argument Ranges
In pow(A, B), if A is negative and finite, and B is finite, B must be an integer, or else the result is NaN.
If A or B are infinite or 0, the following tables give the results:
| A is −∞ | A is 0⁻ | A is 0⁺ | A is +∞ | |
|---|---|---|---|---|
| B is −finite | 0⁻ if B is an odd integer, 0⁺ otherwise | −∞ if B is an odd integer, +∞ otherwise | +∞ | 0⁺ |
| B is 0 | always 1 | |||
| B is +finite | −∞ if B is an odd integer, +∞ otherwise | 0⁻ if B is an odd integer, 0⁺ otherwise | 0⁺ | +∞ |
| A is < -1 | A is -1 | -1 < A < 1 | A is 1 | A is > 1 | |
|---|---|---|---|---|---|
| B is +∞ | result is +∞ | result is NaN | result is 0⁺ | result is NaN | result is +∞ |
| B is −∞ | result is 0⁺ | result is NaN | result is +∞ | result is NaN | result is 0⁺ |
In sqrt(A), if A is +∞, the result is +∞. If A is 0⁻, the result is 0⁻. If A is less than 0, the result is NaN.
In hypot(A, …), if any of the inputs are infinite, the result is +∞.
In log(A, B), if B is 1 or negative, B values between 0 and 1, or greater than 1, are valid. the result is NaN. If A is negative, the result is NaN. If A is 0⁺ or 0⁻, the result is −∞. If A is 1, the result is 0⁺. If A is +∞, the result is +∞.
In exp(A), if A is +∞, the result is +∞. If A is −∞, the result is 0⁺.
(See § 10.9 Type Checking for details on how math functions handle NaN and infinities.)
The only divergences from the behavior of the equivalent JS functions are that NaN is "infectious" in every function, forcing the function to return NaN if any argument calculation is NaN.
Details of the JS Behavior
There are two cases in JS where a NaN is not "infectious" to the math function it finds itself in:
-
Mathwill return. hypot( Infinity , NaN ) Infinity -
Mathwill return. pow( NaN , 0 ) 1
The logic appears to be that,
if you replace the NaN with any Number,
the return value will be the same.
However, this logic is not applied consistently to the Math functions: Math returns Math.
Because this is an error corner case, JS isn’t consistent on the matter, and NaN recognition/handling of calculations is likely done at a higher CSS level rather than in the internal math functions anyway, consistency in CSS was chosen to be more important, so all functions were defined to have "infectious" NaN.
10.6. Sign-Related Functions: abs(), sign()
The sign-related functions—abs() and sign()—compute various functions related to the sign of their argument.
The abs(A) function contains one calculation A, and returns the absolute value of A, as the same type as the input: if A’s numeric value is positive or 0⁺, just A again; otherwise -1 * A.
The sign(A) function contains one calculation A, and returns -1 if A’s numeric value is negative, +1 if A’s numeric value is positive, 0⁺ if A’s numeric value is 0⁺, and 0⁻ if A’s numeric value is 0⁻. The return type is a <number>, made consistent with the input calculation’s type.
Note: Both of these functions operate on the fully simplified/resolved form of their arguments, which may give unintuitive results at first glance. In particular, an expression like 10% might be positive or negative once it’s resolved, depending on what value it’s resolved against. For example, in background-position positive percentages resolve to a negative length, and vice versa, if the background image is larger than the background area. Thus sign(10%) might return 1 or -1, depending on how the percentage is resolved! (Or even 0, if it’s resolved against a zero length.)
10.7. Numeric Keywords
Keywords in calculations provide access to values that are difficult or impossible to represent as literals. Each keyword defines its value, its type, and when it can be resolved.
10.7.1. Numeric Constants: e, pi
While the trigonometric and exponential functions handle many complex numeric operations, some reasonable calculations must be put together more manually, and many times these include well-known constants, such as e and π.
Rather than require authors to manually type out several digits of these constants, a few of them are provided directly:
- e
-
the base of the natural logarithm, approximately equal to 2.7182818284590452354.
- pi
-
the ratio of a circle’s circumference to its diameter, approximately equal to 3.1415926535897932.
Both of these keywords are <number>s, and resolve at parse time.
Note: These keywords are only usable within a calculation, such as calc(pow(e, pi) - pi), or min(pi, 5, e). If used outside of a calculation, they’re treated like any other keyword: animation-name: pi; refers to an animation named "pi"; line-height: e; is invalid (not similar to line-height: 2.7, but line-height: calc(e); is).
10.7.2. Degenerate Numeric Constants: infinity, -infinity, NaN
When a calculation or a subtree of a calculation becomes infinite or NaN, representing it with a numeric value is no longer possible. To aid in serialization of these degenerate values, the following additional math constants are defined:
- infinity
-
the value positive infinity (+∞)
- -infinity
-
the value negative infinity (−∞)
- NaN
-
the value NaN
All of these keywords are <number>s, and resolve at parse time.
As usual for CSS keywords, these are ASCII case-insensitive. Thus, calc(InFiNiTy) is perfectly valid. However, NaN must be serialized with this canonical casing.
Note: As these keywords are <number>s, to get an infinite length, for example, requires an expression like calc(infinity * 1px).
Note: These constants are defined mostly to make serialization of infinite/NaN values simpler and more obvious, but can be used to indicate a "largest possible value", since an infinite value gets clamped to the allowed range. It’s rare for this to be reasonable, but when it is, using infinity is clearer in its intent than just putting an enormous number in one’s stylesheet.
10.7.3. Numeric Variables
Other specifications can define additional keywords which are usable in calculations in certain contexts. For example, relative color syntax defines a number of color-channel keywords representing the value of each color channel as a <number>.
Each specifications defining such keywords must define for each keyword:
-
its value
-
when it resolves (parse time, computed-value time, or used-value time)
10.8. Syntax
The syntax of a math function is:
<calc () > =calc ( <calc-sum>) <min () > =min ( <calc-sum>#) <max () > =max ( <calc-sum>#) <clamp () > =clamp ( [ <calc-sum> | none] , <calc-sum>, [ <calc-sum> | none] ) <round () > =round ( <rounding-strategy>?, <calc-sum>, <calc-sum>?) <mod () > =mod ( <calc-sum>, <calc-sum>) <rem () > =rem ( <calc-sum>, <calc-sum>) <sin () > =sin ( <calc-sum>) <cos () > =cos ( <calc-sum>) <tan () > =tan ( <calc-sum>) <asin () > =asin ( <calc-sum>) <acos () > =acos ( <calc-sum>) <atan () > =atan ( <calc-sum>) <atan2 () > =atan2 ( <calc-sum>, <calc-sum>) <pow () > =pow ( <calc-sum>, <calc-sum>) <sqrt () > =sqrt ( <calc-sum>) <hypot () > =hypot ( <calc-sum>#) <log () > =log ( <calc-sum>, <calc-sum>?) <exp () > =exp ( <calc-sum>) <abs () > =abs ( <calc-sum>) <sign () > =sign ( <calc-sum>) <calc-sum> = <calc-product>[ [ '+' |'-' ] <calc-product>] * <calc-product> = <calc-value>[ [ '*' |'/' ] <calc-value>] * <calc-value> = <number> | <dimension> | <percentage> | <calc-keyword> |( <calc-sum>) <calc-keyword> = e | pi | infinity | -infinity | NaN <rounding-strategy> = nearest | up | down | to-zero
In some contexts, additional <calc-keyword> values can be defined to be valid. (For example, in relative color syntax, appropriate channel keywords are allowed.)
In addition, whitespace is required on both sides of the + and - operators. (The * and / operators can be used without white space around them.)
Several of the math functions above have additional constraints on what their <calc-sum> arguments can contain. Check the definitions of the individual functions for details.
UAs must support calculations of at least 32 <calc-value> terms and at least 32 levels of nesting (parentheses and/or functions). For functions that support an arbitrary number of arguments (such as min()), it must also support at least 32 arguments. If a calculation contains more than the supported number of terms, arguments, or nesting it must be treated as if it were invalid.
10.9. Type Checking
A math function can be many possible types, such as <length>, <number>, etc., depending on the calculations it contains, as defined below. It can be used anywhere a value of that type is allowed.
Additionally, math functions that resolve to <number> can be used in any place that only accepts <integer>; the value is rounded to the nearest integer as it resolves.
Operators form sub-expressions, which gain types based on their arguments.
Note: In previous versions of this specification, multiplication and division were limited in what arguments they could take, to avoid producing more complex intermediate results (such as 1px * 1em, which is <length>²) and to make division-by-zero detectable at parse time. This version now relaxes those restrictions.
-
At a + or - sub-expression, attempt to add the types of the left and right arguments. If this returns failure, the entire calculation’s type is failure. Otherwise, the sub-expression’s type is the returned type.
-
At a * sub-expression, multiply the types of the left and right arguments. The sub-expression’s type is the returned result.
-
At a / sub-expression, let left type be the result of finding the types of its left argument, and right type be the result of finding the types of its right argument and then inverting it.
The sub-expression’s type is the result of multiplying the left type and right type.
-
Anything else is a terminal value, whose type is determined based on its CSS type. (Unless otherwise specified, the type’s associated percent hint is null.)
- <number>
- <integer>
-
the type is «[ ]» (empty map)
- <length>
-
the type is «[ "length" → 1 ]»
- <angle>
-
the type is «[ "angle" → 1 ]»
- <time>
-
the type is «[ "time" → 1 ]»
- <frequency>
-
the type is «[ "frequency" → 1 ]»
- <resolution>
-
the type is «[ "resolution" → 1 ]»
- <flex>
-
the type is «[ "flex" → 1 ]»
- <calc-keyword>
-
the type is as defined by the keyword
- <percentage>
-
If, in the context in which the math function containing this calculation is placed, <percentage>s are resolved relative to another type of value (such as in width, where <percentage> is resolved against a <length>), and that other type is not <number>, the type is determined as the other type, but with a percent hint set to that other type.
Otherwise, the type is «[ "percent" → 1 ]».
- anything else
-
The calculation’s type is failure.
- <number>
-
If both base and input have different non-null percent hints, they can’t be made consistent. Return failure.
-
If base has a null percent hint set base’s percent hint to input’s percent hint.
-
Return base.
Math functions themselves have types, according to their contained calculations:
- calc()
- abs()
-
The type of its contained calculation.
- min()
- max()
- clamp()
- hypot()
- round()
- mod()
- rem()
- max()
-
The result of adding the types of its comma-separated calculations.
- asin()
- acos()
- atan()
- atan2()
- acos()
-
«[ "angle" → 1 ]».
- sign()
- sin()
- cos()
- tan()
- pow()
- sqrt()
- log()
- exp()
- sin()
-
«[ ]» (empty map).
For each of the above, if the type is failure, the math function is invalid.
A math function resolves to <number>, <length>, <angle>, <time>, <frequency>, <resolution>, <flex>, or <percentage> according to which of those productions its type matches. (These categories are mutually exclusive.) If it can’t match any of these, the math function is invalid.
Note: Algebraic simplifications do not affect the validity of a math function or its resolved type. For example, calc(5px - 5px + 10s) and calc(0 * 5px + 10s) are both invalid due to the attempt to add a length and a time.
Note: Note that <percentage>s relative to <number>s, such as in opacity, are not combinable with those numbers—opacity: calc(.25 + 25%) is invalid. Allowing this causes significant problems with "unit algebra" (allowing multiplication/division of <dimension>s), and in every case so far, doesn’t provide any new functionality. (For example, opacity: 25% is identical to opacity: .25; it’s just a trivial syntax transform.) You can still perform other operations with them, such as opacity: calc(100% / 3);, which is valid.
Note: Because <number-token>s are always interpreted as <number>s or <integer>s, "unitless 0" <length>s aren’t supported in math functions. That is, width: calc(0 + 5px); is invalid, because it’s trying to add a <number> to a <length>, even though both width: 0; and width: 5px; are valid.
Note: Although there are a few properties in which a bare <number> becomes a <length> at used-value time (specifically, line-height and tab-size), <number>s never become "length-like" in calc(). They always stay as <number>s.
Note: In Quirks Mode [QUIRKS], some properties that would normally only accept <length>s are defined to also accept <number>s, interpreting them as px lengths. Like unitless zeroes, this has no effect on the parsing or behavior of math functions, though a math function that resolves to a <number> value might become valid in Quirks Mode (and have its result interpreted as a px length).
10.9.1. Infinities, NaN, and Signed Zero
Math functions follow IEEE-754 semantics, which means they recognize the concepts of positive and negative zero, positive and negative infinity, and NaN (not a number).
However, these concepts are only retained within a calculation tree; if a top-level calculation (a math function not nested directly inside of another math function) would result in one of these special values, they’re instead "censored" into a standard representable value, as defined below.
Signed zeros (indicated here as 0⁺ or 0⁻) can not be written directly in CSS; 0, +0 and -0 all produce the standard "unsigned" zero, which is considered positive (0⁺) for the purposes of these rules.
Signed zeroes are produced in the following ways:
-
Negative zero (0⁻) can be produced by a multiplication or division that produces zero with exactly one negative argument (such as -5 * 0 or 1 / -infinity).
-
0⁻ + 0⁻ or 0⁻ - 0⁺ produces 0⁻. All other additions or subtractions that would produce a zero produce 0⁺.
-
Multiplying or dividing 0⁻ with a positive number (including 0⁺) produces a negative result (either 0⁻ or −∞), while multiplying or dividing 0⁻ with a negative number produces a positive result.
(In other words, multiplying or dividing with 0⁻ follows standard sign rules.)
-
When comparing 0⁺ and 0⁻, 0⁻ is less than 0⁺. For example, min(0⁺, 0⁻) must produce 0⁻, max(0⁺, 0⁻) must produce 0⁺, and clamp(0⁺, 0⁻, 1) must produce 0⁺.
-
Certain argument combinations in math functions are defined to produce 0⁻ (for example, round(-1, infinity)). All other operations that produce a zero produce positive zero (0⁺).
Signed zeroes do not escape a top-level calculation; they’re censored into the "unsigned" zero.
Infinities (indicated here as +∞ or −∞) can be written directly using the math constants infinity and -infinity, or produced as a result of some calculations:
-
Dividing a value by zero produces either +∞ or −∞, according to the standard sign rules.
-
Adding or subtracting ±∞ to anything produces the appropriate infinity.
-
Multiplying any value by ±∞ produces the appropriate infinity.
-
Dividing any value by ±∞ produces zero.
-
Certain argument combinations in math functions are defined to produce infinities (for example, pow(0, -1) produces +∞).
Note: The rules for producing NaN, below, supersede the above rules for producing infinities.
Infinities do not escape a top-level calculation; they’re clamped to the minimum or maximum value allowed in the context, as defined in § 10.12 Range Checking.
NaN (short for "not a number") is the result of certain operations that don’t have a well-defined value. It can be written directly using the math constants NaN, or produced as a result of some calculations:
-
Dividing zero by zero, dividing ±∞ by ±∞, multiplying 0 by ±∞, adding +∞ to −∞, or subtracting two infinities of the same sign produces NaN.
These rules override any other result, if there’s a conflict. For example, 0 / 0 is NaN, not +∞.
-
Certain argument combinations in math functions are defined to produce NaN (for example, asin(2) produces NaN).
-
Any operation with at least one NaN argument produces NaN.
NaN does not escape a top-level calculation; it’s censored into a zero value
On the other hand, calc(1 / calc(-5 * 0)) produces −∞, same as calc(1 / (-5 * 0))—the inner calc resolves to 0⁻, and as it’s not a top-level calculation, it passes it up unchanged to the outer calc to produce −∞. If it was censored into an unsigned zero, it would instead produce +∞.
10.10. Internal Representation
The internal representation of a math function is a calculation tree: a tree where the branch nodes are operator nodes corresponding either to math functions (such as Min, Cos, Sqrt, etc) or to operators in a calculation (Sum, Product, Negate, and Invert, the calc-operator nodes), and the leaf nodes are either numeric values (such as numbers, dimensions, and percentages) or non-math functions that resolve to a numeric type.
Math functions are turned into calculation trees depending on the function:
- calc()
-
The internal representation of a calc() function is the result of parsing a calculation from its argument.
- any other math function
-
The internal representation is an operator node with the same name as the function, whose children are the result of parsing a calculation from each of the function’s arguments, in the order they appear.
-
Discard any <whitespace-token>s from values.
-
An item in values is an “operator” if it’s a <delim-token> with the value "+", "-", "*", or "/". Otherwise, it’s a “value”.
-
Collect children into Product and Invert nodes.
For every consecutive run of value items in values separated by "*" or "/" operators:
-
For each "/" operator in the run, replace its right-hand value item rhs with an Invert node containing rhs as its child.
-
Replace the entire run with a Product node containing the value items of the run as its children.
-
-
Collect children into Sum and Negate nodes.
-
For each "-" operator item in values, replace its right-hand value item rhs with a Negate node containing rhs as its child.
-
If values has only one item, and it is a Product node or a parenthesized simple block, replace values with that item.
Otherwise, replace values with a Sum node containing the value items of values as its children.
-
-
At this point values is a tree of Sum, Product, Negate, and Invert nodes, with other types of values at the leaf nodes. Process the leaf nodes.
For every leaf node leaf in values:
-
If leaf is a parenthesized simple block, replace leaf with the result of parsing a calculation from leaf’s contents.
-
If leaf is a math function, replace leaf with the internal representation of that math function.
-
-
Return the result of simplifying a calculation tree from values.
10.10.1. Simplification
Internal representations of math functions are eagerly simplified to the extent possible, using standard algebraic simplifications (distributing multiplication over sums, combining similar units, etc.).
When used in non-property contexts (such as in @font-face descriptors, for example), math functions are simplified as if they were specified values.
-
If root is a numeric value:
-
If root is a percentage that will be resolved against another value, and there is enough information available to resolve it, do so, and express the resulting numeric value in the appropriate canonical unit. Return the value.
-
If root is a dimension that is not expressed in its canonical unit, and there is enough information available to convert it to the canonical unit, do so, and return the value.
-
If root is a <calc-keyword> that can be resolved, return what it resolves to, simplified.
-
Otherwise, return root.
-
-
If root is any other leaf node (not an operator node):
-
If there is enough information available to determine its numeric value, return its value, expressed in the value’s canonical unit.
-
Otherwise, return root.
-
-
At this point, root is an operator node. Simplify all the calculation children of root.
-
If root is an operator node that’s not one of the calc-operator nodes, and all of its calculation children are numeric values with enough information to compute the operation root represents, return the result of running root’s operation using its children, expressed in the result’s canonical unit.
If a percentage is left at this point, it will usually block simplification of the node, since it needs to be resolved against another value using information not currently available. (Otherwise, it would have been converted to a different value in an earlier step.) This includes operations such as "min", since percentages might resolve against a negative basis, and thus end up with an opposite comparative relationship than the raw percentage value would seem to indicate.
However, "raw" percentages—ones which do not resolve against another value, such as in opacity—might not block simplification.
-
If root is a Min or Max node, attempt to partially simplify it:
-
For each node child of root’s children:
If child is a numeric value with enough information to compare magnitudes with another child of the same unit (see note in previous step), and there are other children of root that are numeric values with the same unit, combine all such children with the appropriate operator per root, and replace child with the result, removing all other child nodes involved.
-
If root has only one child, return the child.
Otherwise, return root.
-
-
If root is a Negate node:
-
If root’s child is a numeric value, return an equivalent numeric value, but with the value negated (0 - value).
-
If root’s child is a Negate node, return the child’s child.
-
Return root.
-
-
If root is an Invert node:
-
If root’s child is a number (not a percentage or dimension) return the reciprocal of the child’s value.
-
If root’s child is an Invert node, return the child’s child.
-
Return root.
-
-
If root is a Sum node:
-
For each of root’s children that are Sum nodes, replace them with their children.
-
For each set of root’s children that are numeric values with identical units, remove those children and replace them with a single numeric value containing the sum of the removed nodes, and with the same unit.
(E.g. combine numbers, combine percentages, combine px values, etc.)
-
If root has only a single child at this point, return the child. Otherwise, return root.
Note: Zero-valued terms cannot be simply removed from a Sum; they can only be combined with other values that have identical units. (This is because the mere presence of a unit, even with a zero value, can sometimes imply a change in behavior.)
-
-
If root is a Product node:
-
For each of root’s children that are Product nodes, replace them with their children.
-
If root has multiple children that are numbers (not percentages or dimensions), remove them and replace them with a single number containing the product of the removed nodes.
-
If root contains only two children, one of which is a number (not a percentage or dimension) and the other of which is a Sum whose children are all numeric values, multiply all of the Sum’s children by the number, then return the Sum.
-
If root contains only numeric values and/or Invert nodes containing numeric values, and multiplying the types of all the children (noting that the type of an Invert node is the inverse of its child’s type) results in a type that matches any of the types that a math function can resolve to, return the result of multiplying all the values of the children (noting that the value of an Invert node is the reciprocal of its child’s value), expressed in the result’s canonical unit.
-
Return root.
-
10.11. Computed Value
The computed value of a math function is its calculation tree simplified, using all the information available at computed value time. (Such as the em to px ratio, how to resolve percentages in some properties, etc.)
Where percentages are not resolved at computed-value time, they are not resolved in math functions, e.g. calc(100% - 100% + 1px) resolves to calc(0% + 1px), not to 1px. If there are special rules for computing percentages in a value (e.g. the height property), they apply whenever a math function contains percentages.
The calculation tree is again simplified at used value time; with used value time information, a math function always simplifies down to a single numeric value.
Due to this, background-position computation preserves the percentage in a calc() whereas font-size will compute such expressions directly into a length.
Given the complexities of width and height calculations on table cells and table elements, math expressions mixing both percentages and non-zero lengths for widths and heights on table columns, table column groups, table rows, table row groups, and table cells in both auto and fixed layout tables MUST be treated as if auto had been specified.
10.12. Range Checking
Parse-time range-checking of values is not performed within math functions, and therefore out-of-range values do not cause the declaration to become invalid. However, the value resulting from a top-level calculation must be clamped to the range allowed in the target context. Clamping is performed on computed values to the extent possible, and also on used values if computation was unable to sufficiently simplify the expression to allow range-checking. (Clamping is not performed on specified values.)
Note: This requires all contexts accepting calc() to define their allowable values as a closed (not open) interval.
Note: By definition, ±∞ are outside the allowed range for any property, and will clamp to the minimum/maximum value allowed. Even properties that can explicitly represent infinity as a keyword value, such as animation-iteration-count, will end up clamping ±∞, as math functions can’t resolve to keyword values; the numeric part of the property’s syntax still has a minimum/maximum value.
Additionally, if a math function that resolves to <number> is used somewhere that only accepts <integer>, the computed value and used value are rounded to the nearest integer, in the same manner as clamping, above.
width : calc ( 5 px -10 px ); width : calc ( -5 px ); width : 0 px ;
Note however that width: -5px is not equivalent to width: calc(-5px)! Out-of-range values outside calc() are syntactically invalid, and cause the entire declaration to be dropped.
10.13. Serialization
This section is still under discussion.
-
If the root of the calculation tree fn represents is a numeric value (number, percentage, or dimension), and the serialization being produced is of a computed value or later, then clamp the value to the range allowed for its context (if necessary), then serialize the value as normal and return the result.
-
If fn represents an infinite or NaN value:
-
Let s be the string "calc(".
-
Serialize the keyword infinity, -infinity, or NaN, as appropriate to represent the value, and append it to s.
-
If fn’s type is anything other than «[ ]» (empty, representing a <number>), append " * " to s. Create a numeric value in the canonical unit for fn’s type (such as px for <length>), with a value of 1. Serialize this numeric value and append it to s.
-
Return s.
-
-
If the calculation tree’s root node is a numeric value, or a calc-operator node, let s be a string initially containing "calc(".
Otherwise, let s be a string initially containing the name of the root node, lowercased (such as "sin" or "max"), followed by a "(" (open parenthesis).
-
For each child of the root node, serialize the calculation tree. If a result of this serialization starts with a "(" (open parenthesis) and ends with a ")" (close parenthesis), remove those characters from the result. Concatenate all of the results using ", " (comma followed by space), then append the result to s.
-
Append ")" (close parenthesis) to s.
-
Return s.
-
Let root be the root node of the calculation tree.
-
If root is a numeric value, or a non-math function, serialize root per the normal rules for it and return the result.
-
If root is anything but a Sum, Negate, Product, or Invert node, serialize a math function for the function corresponding to the node type, treating the node’s children as the function’s comma-separated calculation arguments, and return the result.
-
If root is a Negate node, let s be a string initially containing "(-1 * ".
Serialize root’s child, and append it to s.
Append ")" to s, then return it.
-
If root is an Invert node, let s be a string initially containing "(1 / ".
Serialize root’s child, and append it to s.
Append ")" to s, then return it.
-
If root is a Sum node, let s be a string initially containing "(".
Serialize root’s first child, and append it to s.
For each child of root beyond the first:
-
If child is a Negate node, append " - " to s, then serialize the Negate’s child and append the result to s.
-
If child is a negative numeric value, append " - " to s, then serialize the negation of child as normal and append the result to s.
-
Otherwise, append " + " to s, then serialize child and append the result to s.
Finally, append ")" to s and return it.
-
-
If root is a Product node, let s be a string initially containing "(".
Serialize root’s first child, and append it to s.
For each child of root beyond the first:
-
If child is an Invert node, append " / " to s, then serialize the Invert’s child and append the result to s.
-
Otherwise, append " * " to s, then serialize child and append the result to s.
Finally, append ")" to s and return it.
-
-
Let ret be an empty list.
-
If nodes contains a number, remove it from nodes and append it to ret.
-
If nodes contains a percentage, remove it from nodes and append it to ret.
-
If nodes contains any dimensions, remove them from nodes, sort them by their units, ordered ASCII case-insensitively, and append them to ret.
-
If nodes still contains any items, append them to ret in the same order.
-
Return ret.
Tests
- calc-rgb-percent-001.html (live test) (source)
- calc-serialization.html (live test) (source)
- calc-serialization-002.html (live test) (source)
- getComputedStyle-border-radius-001.html (live test) (source)
- getComputedStyle-border-radius-003.html (live test) (source)
- calc-background-position-003.html (live test) (source)
A value like calc(20px + 0%) would serialize as calc(0% + 20px), maintaining both terms in the serialized value. (It’s important to maintain zero-valued terms, so the calc() doesn’t suddenly "change shape" in the middle of a transition when one of the values happens to have a zero value temporarily. This also removes the need to "pick a unit" when all the terms are zero.)
A value like calc(20px + 2em) would serialize as calc(2em + 20px) as a specified value (maintaining both units as they’re incompatible at specified-value time, but sorting them alphabetically), or as something like 52px as a computed value (em values are converted to absolute lengths at computed-value time, so assuming 1em = 16px, they combine into 52px, which then drops the calc() wrapper.)
When used in non-property contexts (such as in @font-face descriptors, for example), math functions are simplified as if they were specified values.
See [CSSOM] for further information on serialization.
10.14. Combination of Math Functions
Interpolation of math functions, with each other or with numeric values and other numeric-valued functions, is defined as Vresult = calc((1 - p) * VA + p * VB). (Simplification of the value might then reduce the expression to a smaller, simpler form.)
Addition of math functions, with each other or with numeric values and other numeric-valued functions, is defined as Vresult = calc(VA + VB). (Simplification of the value might then reduce the expression to a smaller, simpler form.)
Appendix A: Coordinating List-Valued Properties
Some list-valued properties have coordinated effects: each item in their value list applies to a distinct effect, and corresponding entries in each property’s list all refer to the same effect. Often the coordinating values can also be specified together as a single entry in a list-valued shorthand property.
A typical example is the list-valued background-* properties, which can specify multiple background image layers. For each property controlling how the image is sized, tiled, placed, etc., the Nth item in its list describes some effect that applies to the Nth background image.
A coordinating list property group creates a coordinated value list, which has, for each entry, a value from each property in the group; these are used together to define a single effect, such as a background image layer or an animation. The coordinated value list is assembled as follows:
-
The length of the coordinated value list is determined by the number of items specified in one particular coordinating list property, the coordinating list base property. (In the case of backgrounds, this is the background-image property.)
-
The Nth value of the coordinated value list is constructed by collecting the Nth use value of each coordinating list property
-
If a coordinating list property has too many values specified, excess values at the end of its list are not used.
-
If a coordinating list property has too few values specified, its value list is repeated to add more used values.
-
The computed values of the coordinating list properties are not affected by such truncation or repetition.
Appendix B: IANA Considerations
Registration for the about : invalid
This sections defines and registers the
The official record of this registration can be found at http://www.iana.org/assignments/about-uri-tokens/about-uri-tokens.xhtml.
| Registered Token | invalid
|
|---|---|
| Intended Usage | The |
| Contact/Change controller | CSS WG <www-style@w3.org> (on behalf of W3C) |
| Specification | CSS Values and Units Module Level 3 |
Appendix C: Quirky Lengths
When CSS is being parsed in quirks mode, <quirky-length> is a type of <length> that is only valid in certain properties:
It is not valid in properties that include or reference these properties, such as the background shorthand, or inside functional notations such as calc(), except that they must be allowed in rect() in the clip property.
Additionally, while <quirky-length> must be valid as a <length> when parsing the affected properties in the @supports rule,
it is not valid for those properties
when used in the CSS.supports() method.
A <quirky-length> is syntactically identical to a <number-token>, and is interpreted as a px length with the same value.
(In other words, Quirks Mode allows all px lengths in the affected properties to be written without a unit, similar to unitless zero lengths.)
Acknowledgments
Firstly, the editors would like to thank all of the contributors to the previous level of this module.
Secondly, we would like to acknowledge Anthony Frehner, Emilio Cobos Álvarez, Koji Ishii, Noam Rosenthal, and Xidorn Quan for their comments and suggestions, which have improved Level 4.
Changes
Recent Changes
(This is a subset of Additions Since Level 3.)
Substantial changes since 18 December 2023 WD:
-
Added the none values to clamp(), (Issue 9713)
-
Generally fixed how type inference handles percentages. (Issue 10017)
-
Restored dependency of viewport-percentage lengths on overflow: scroll and added one on scrollbar-gutter to make it possible for 100 of these units to actually match the initial containing block. (Issue 6026)
-
Allow B to be omitted in round() if the A’s type is <number>. (Issue 9668)
Substantial changes since 27 October 2023 WD:
-
Pinned the default viewport-percentage units to the large viewport-percentage units—despite violation of the “avoid dataloss by default principle”—given existing interoperability and presumed Web-compat restriction. (Issue 6452)
-
Added an explicit definition for the CSS grammar production block convention. (Issue 2921)
-
Clarified character encoding of percent-encoded URLs. (Issue 9301)
Substantial changes since 6 April 2023 WD:
-
Punted mix() to [css-values-5]. (Issue 9343)
-
Color type defined to be non-additive. (Issue 8576)
-
Non-property contexts treat math functions as specified values. (Issue 7964)
-
Specified that URLs from CSS are always transmitted as UTF-8. (Issue 9301)
-
Fixed addition/accumulation to use the *second* value, when the two values aren’t additive/accumulative. (Issue 9070)
-
Specified that font-relative lengths are always resolved against the parent element when used in a font-* property. (Issue 8169)
-
Simplify away single-argument min() and max() functions. (Issue 9559)
Substantial changes since 19 October 2022 WD:
- Added § 2.6 Functional Notation Definitions to formally define the way that functional notation syntaxes are defined. (Issue 2921)
- Added algorithm for snap as a border width, to reflect the interoperable rules for rendering consistent stroke widths. (Issue 5210)
- Clarified grammar and computed value of mix(). (Issue 8096)
- Undefined the behavior of tan() at the asymptote values. (Issue 8527)
- Specified that negative <resolution> values are out-of-range by definition. (Issue 8532)
- Clarified that fully omitted mix() arguments are valid. (Issue 8556)
- Clarified that range clamping happens specifically to top-level calculations (rather than the unclear term "expressions"). (Issue 8158)
- Added formal definitions for <url()> and <src()> (in addition to <url>).
- Rephrased fragment-only URLs in terms of tree-scoped references. (Issue 3320)
Substantial changes since 16 December 2021 WD:
- Changed resolution of a url() with the local url flag to reference the current node tree (regardless of document base URL modifications). (Issue 3320)
- Switched censoring of NaN that escapes a math function from infinity to zero. (Issue 7067)
- Added Appendix A: Coordinating List-Valued Properties to allow this property pattern to be easily referenced. (Issue 7164)
- Restricted mix() to be the sole value of a declaration. (Issue 6700)
- Updated to match latest Fetch terminology. (Fetch PR 1413, CSS PR 7160)
- Clarified that the font-relative lengths are calculated without text shaping.
- Defined serialization of empty urls to be
url ( "" ) - Defined serialization of <position> specified values. (Issue 2274)
- Fixed definition of numbers to allow decimals in combination with scientific notation, as originally intended and as defined in [CSS-SYNTAX-3]. (Issue 7248)
- Corrected various functions to return an empty map for their type instead of «[ "number" → 1 ]». (Issue 7486)
- Clarified effect of special UA restrictions on line-height on lh and rlh. (Issue 3257)
- Defined
<notation to refer to functional notations. (Issue 5728)function () >
Substantial changes since 16 October 2021 WD:
- Switched *vi and *vb units to resolve against the computed writing mode of the element itself. (Issue 6873)
- Added § 4.5.4 URL Processing Model to define integration with CORS, etc. (Issue 562)
-
Fixed the inverted assignment of viewport-percentage length behaviors
to types of interface changes (A vs. B).
-
Changes in interface that happen as a result of scrolling
or other frequent page interactions that would disturb the user
if they resulted in substantial layout changes
must be categorized as the
former (A)latter (B) . -
Changes in interface that have a sufficiently steady state
that re-laying out the document into the adjusted space
would be beneficial to the user
must be categorized as the
latter (B)former (A) .
-
Changes in interface that happen as a result of scrolling
or other frequent page interactions that would disturb the user
if they resulted in substantial layout changes
must be categorized as the
- Defined minimum number of calc() terms, arguments, and nesting as 32. (Issue 3462)
- Defined that mod(-0, infinity) returns NaN. (Issue 4723)
- Deferred toggle() and attr() to Level 5.
Changes since 30 September 2021 WD:
- Added rex, rcap, rch, and ric units.
- Switched toggle() to use semicolons, matching with mix(). (Issue 6701)
- Fixed some wording errors in the definition of calc(). (Issue 6506)
- Imported definition of <quirky-length> from [QUIRKS]. (Issue 6100)
Changes since 7 July 2021 WD:
- Added mix() notation for representing interpolated values.
- Defined generically the computation of <integer>, <number>, <percentage>, and <length>.
- Clarified that only non-zero lengths create a percentage+length mix that switches table cells to auto sizing.
Changes since 11 November 2020 WD:
- Updated interpolation of colors to reference [CSS-COLOR-4] instead of [CSS-COLOR-3].
- Added the svh, svw, svi, svb, svmin, and svmax small viewport-percentage units; lvh, lvw, lvi, lvb, lvmin, and lvmax large viewport-percentage units; and dvh, dvw, dvi, dvb, dvmin, and dvmax dynamic viewport-percentage units. (Issue 4329 and Issue 6113)
- Clamped excessively large <angle> values to multiples of 360deg. (Issue 6105)
- Added back rules on range-checking combined values lost during move from the CSS Transitions specification. (Issue 6097)
- Specified that UA-imposed minimum font sizes apply to the used font-size and not to resolution of font-relative lengths. (Issue 5858)
- Clarified how min() and max() percentages can partially simplify. (Issue 6293)
Additions Since Level 3
Changes since CSS Values and Units Level 3:
- Explicitly undefined numeric precision/range.
- Added rules for interpolation per value type, and their clarified computed values.
- Updated interpolation of colors to reference [CSS-COLOR-4].
Additions since CSS Values and Units Level 3:
- Defined the <dashed-ident> type.
- Defined the <ratio> type.
- Added src() to the <url> type.
- Added the vi, vb, ic, cap, lh and rlh length units.
- Added the svh, svw, svi, svb, svmin, and svmax small viewport-percentage units and dvh, dvw, dvi, dvb, dvmin, and dvmax dynamic viewport-percentage units.
- Added the x alias to dppx.
- Added min(), max(), and clamp() comparison functions.
- Added round(), mod(), rem(), sin(), cos(), tan(), asin(), acos(), atan(), atan2(), pow(), sqrt(), hypot(), log(), exp(), abs(), sign() math functions.
- Added e, pi, infinity, -infinity, NaN constants for use in calc().
- Added unit algebra to calc(), allowing multiplication and division of dimensions.
- A non-integer in a calc() automatically rounds to the nearest integer when used where an <integer> is required.
- Defined serialization of math functions.
- Added a genericized definition of coordinating list property groups, to make it easier to reference the coordinating behavior of the background properties.
Security Considerations
This specification presents no new security considerations.
This specification defines the url() and src() functions (<url>), which allow CSS to make network requests. Depending on what features they are used in, these can potentially expose whether or not the user has access to resources on a network, and expose information about their contents (such as the rules within a style sheet, the size of an image, the metrics of a font). They can also allow exfiltrating data via URL.
Privacy Considerations
This specification defines units that expose the user’s screen size (the viewport-percentage lengths), default font size, and potentially some information about which fonts are available on the user’s system (the font-relative lengths).
This specification defines the url() and src() functions (<url>), which allow CSS to make network requests. Depending on what features they are used in, these can potentially expose whether or not the user has access to resources on a network, and expose information about their contents (such as the rules within a style sheet, the size of an image, the metrics of a font). They can also allow exfiltrating data via URL.